|
Sei 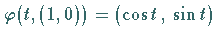 eine
eine 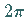 -periodische Lösung von
(17.9a).
Die Matrix -periodische Lösung von
(17.9a).
Die Matrix 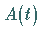 der Variationsgleichung lautet
der Variationsgleichung lautet
Die bei  normierte Fundamentalmatrix
normierte Fundamentalmatrix 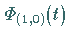 ist
wobei das letzte Produkt eine FLOQUET-Darstellung von
ist
wobei das letzte Produkt eine FLOQUET-Darstellung von 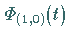 darstellt.
Also ist
darstellt.
Also ist 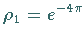 und
und 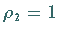 .
Die Multiplikatoren lassen sich auch ohne FLOQUET-Darstellung bestimmen.
Für System (17.9a) ist div .
Die Multiplikatoren lassen sich auch ohne FLOQUET-Darstellung bestimmen.
Für System (17.9a) ist div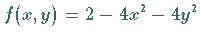 .
Damit ergibt sich div .
Damit ergibt sich div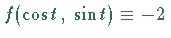 .
Nach obiger Formel ist .
Nach obiger Formel ist 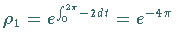 . .
| ![]() die Multiplikatoren des
periodischen Orbits
die Multiplikatoren des
periodischen Orbits ![]() ,
und sei
,
und sei ![]() die Monodromie-Matrix von
die Monodromie-Matrix von
![]() .
Dann gilt
.
Dann gilt
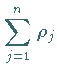
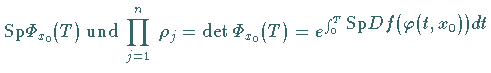
![]() ,
so ist
,
so ist ![]() und
und
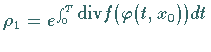 .
.