Klassifizierung und Stabilität der Ruhelagen
Sei 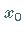 eine Ruhelage von (17.1).
Das lokale Verhalten der Orbits von (17.1) nahe
eine Ruhelage von (17.1).
Das lokale Verhalten der Orbits von (17.1) nahe 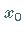 wird, unter gewissen
Voraussetzungen, durch die Variationsgleichung
wird, unter gewissen
Voraussetzungen, durch die Variationsgleichung 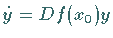 beschrieben, wobei
beschrieben, wobei 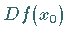 die JACOBI-Matrix von
die JACOBI-Matrix von 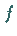 in
in 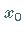 ist.
Besitzt
ist.
Besitzt 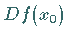 keinen Eigenwert
keinen Eigenwert 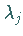 mit Re
mit Re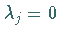 ,
so heißt die
Ruhelage
,
so heißt die
Ruhelage 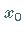 hyperbolisch .
Die hyperbolische Ruhelage
hyperbolisch .
Die hyperbolische Ruhelage 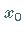 ist vom Typ
ist vom Typ 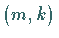 ,
wenn
,
wenn 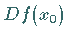 genau
genau 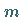 Eigenwerte mit negativem Realteil und
Eigenwerte mit negativem Realteil und 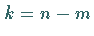 Eigenwerte mit positivem Realteil
besitzt.
Die hyperbolische Ruhelage vom Typ
Eigenwerte mit positivem Realteil
besitzt.
Die hyperbolische Ruhelage vom Typ 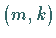 heißt Senke , wenn
heißt Senke , wenn 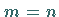 ist,
Quelle , wenn
ist,
Quelle , wenn  ist, und Sattel , wenn
ist, und Sattel , wenn 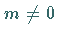 und
und 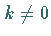 ist
(s. die folgenden Abbildungen).
ist
(s. die folgenden Abbildungen).
Es gilt der folgende
Satz über Stabilität in der ersten Näherung für kontinuierliche dynamische
Systeme:
Eine Senke ist asymptotisch stabil; Quellen und Sattel sind instabil.
Im Rahmen der drei topologischen Grundtypen von hyperbolischen Ruhelagen (Senke, Quelle
und Sattelpunkte) sind weitere algebraische Unterscheidungen üblich.
So heißt eine Senke (Quelle) stabiler Knoten ( instabiler Knoten ), wenn
alle Eigenwerte der JACOBI-Matrix reell sind, und stabiler Strudel
( instabiler Strudel ), wenn Eigenwerte mit nicht verschwindendem Imaginärteil
vorliegen.
Für  ergibt sich daraus eine Einteilung der Sattelpunkte in Sattelknoten
und Sattelstrudel.
ergibt sich daraus eine Einteilung der Sattelpunkte in Sattelknoten
und Sattelstrudel.
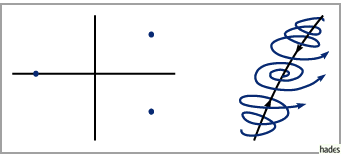
In den folgenden Abbildungen sind für die drei toplogischen Grundtypen jeweils links
die Eigenwerte der JACOBI-Matrix und rechts das Phasenporträt dargestellt.
Senke:

Quelle:
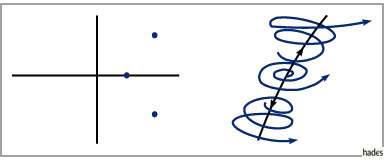
Sattelpunkt:
![]() ergibt sich daraus eine Einteilung der Sattelpunkte in Sattelknoten
und Sattelstrudel.
ergibt sich daraus eine Einteilung der Sattelpunkte in Sattelknoten
und Sattelstrudel.