Lineare Differentialgleichungen mit periodischen Koeffizienten
Betrachtet wird die homogene lineare Differentialgleichung (17.13b),
wobei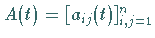 
eine T-periodische Matrix-Funktion ist,
d.h., es gilt 
.
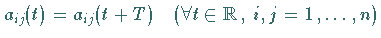In diesem Falle nennt man (17.13b) eine
lineare T-periodische Differentialgleichung .
Dann läßt sich jede Fundamentalmatrix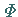 
von
(17.13b) in der Form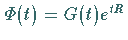 
darstellen,
wobei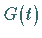 
eine glatte, reguläre 
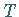-periodische Matrix-Funktion ist und 
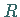eine
konstante Matrix vom Typ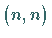 
darstellt ( Satz von FLOQUET).
Sei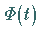 
die bei 
normierte Fundamentalmatrix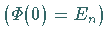 
der 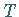-periodischen Differentialgleichung (17.13b) und
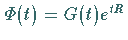eine Darstellung laut Satz von FLOQUET.
Die Matrix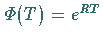 
heißt Monodromie-Matrix von
(17.13b);
die Eigenwerte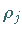 
von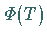 
sind die Multiplikatoren von
(17.13b).
Eine Zahl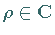 
ist genau dann Multiplikator von
(17.13b), wenn es eine Lösung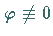 
von
(17.13b) gibt, so daß
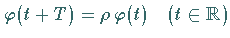gilt.
