|
Betrachtet wird die periodisch gestörte Pendelgleichung
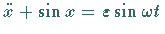 ,
d.h. das System ,
d.h. das System
in der 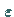 ein kleiner Parameter und
ein kleiner Parameter und 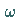 ein weiterer Parameter ist.
Das ungestörte System
ist ein HAMILTON-System mit
ein weiterer Parameter ist.
Das ungestörte System
ist ein HAMILTON-System mit 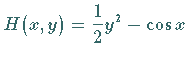 .
Das ungestörte System besitzt (u.a.) ein Paar heterokliner Orbits durch .
Das ungestörte System besitzt (u.a.) ein Paar heterokliner Orbits durch 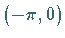 und
und
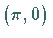 .
Im zylindrischen Phasenraum .
Im zylindrischen Phasenraum 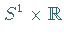 sind dies homokline Orbits, gegeben durch
Die direkte Berechnung der MELNIKOV-Funktion liefert
Da
sind dies homokline Orbits, gegeben durch
Die direkte Berechnung der MELNIKOV-Funktion liefert
Da 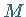 bei
bei 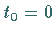 eine einfache Nullstelle besitzt, hat die POINCARÉ-Abbildung
des gestörten Systems für kleine
eine einfache Nullstelle besitzt, hat die POINCARÉ-Abbildung
des gestörten Systems für kleine 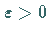 transversale homokline Punkte.
transversale homokline Punkte.
| 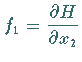 und
und
 ,
wobei
,
wobei
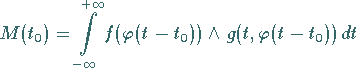
![]() ,
der aus einem Sattel
,
der aus einem Sattel ![]() in einen Sattel
in einen Sattel ![]() läuft.
Seien
läuft.
Seien ![]() und
und ![]() die Sattel der POINCARE-Abbildung
die Sattel der POINCARE-Abbildung
![]() für kleine
für kleine ![]() .
Besitzt
.
Besitzt ![]() ,
berechnet wie oben, in
,
berechnet wie oben, in ![]() eine einfache Nullstelle, so schneiden sich
eine einfache Nullstelle, so schneiden sich
![]() und
und ![]() für kleine
für kleine ![]() transversal.
transversal.
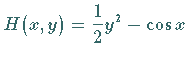 .
Das ungestörte System besitzt (u.a.) ein Paar heterokliner Orbits durch
.
Das ungestörte System besitzt (u.a.) ein Paar heterokliner Orbits durch