|
Gegeben sei im 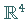 das HAMILTON-System (in Winkel-Wirkungsvariablen)
das HAMILTON-System (in Winkel-Wirkungsvariablen)
wobei die HAMILTON-Funktion 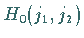 analytisch ist.
Offenbar hat dieses System die Lösungen
mit Konstanten
analytisch ist.
Offenbar hat dieses System die Lösungen
mit Konstanten 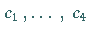 ,
wobei ,
wobei 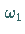 und
und 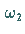 von
von 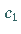 und
und 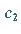 abhängen können.
Die Beziehung
abhängen können.
Die Beziehung 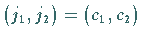 definiert einen invarianten Torus
definiert einen invarianten Torus 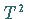 .
Es wird nun anstelle von .
Es wird nun anstelle von  die gestörte HAMILTON-Funktion
betrachtet, wobei
die gestörte HAMILTON-Funktion
betrachtet, wobei 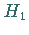 analytisch und
analytisch und 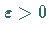 ein kleiner Parameter sei.
ein kleiner Parameter sei.
Das Theorem von KOLMOGOROV-ARNOLD-MOSER (KAM- Theorem )
sagt in dieser Situation aus, daß, falls  nichtdegeniert ist, d.h.
nichtdegeniert ist, d.h.
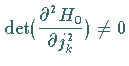 gilt, für hinreichend kleine
gilt, für hinreichend kleine
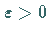 im gestörten HAMILTON-System die Mehrzahl der invarianten
nichtresonanten Tori nicht verschwindet, sondern nur leicht deformiert wird.
Mehrzahl ist in dem Sinne zu verstehen, daß das LEBESGUE-Maß der
bezüglich der Tori gebildeten Komplementmenge gegen Null geht, wenn
im gestörten HAMILTON-System die Mehrzahl der invarianten
nichtresonanten Tori nicht verschwindet, sondern nur leicht deformiert wird.
Mehrzahl ist in dem Sinne zu verstehen, daß das LEBESGUE-Maß der
bezüglich der Tori gebildeten Komplementmenge gegen Null geht, wenn 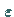 gegen
gegen 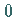 geht.
Ein oben definierter Torus, charakterisiert durch
geht.
Ein oben definierter Torus, charakterisiert durch 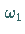 und
und 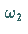 ,
heißt
nichtresonant, wenn es eine Konstante ,
heißt
nichtresonant, wenn es eine Konstante 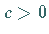 gibt, so daß für alle positiven ganzen
Zahlen
gibt, so daß für alle positiven ganzen
Zahlen 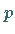 und
und 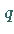 die Ungleichung
die Ungleichung
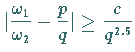 gilt.
gilt.
| 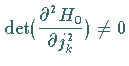 gilt, für hinreichend kleine
gilt, für hinreichend kleine
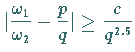 gilt.
gilt.