Betrachtet wird die Differentialgleichung (17.53) im 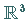 mit einem skalaren
Parameter
mit einem skalaren
Parameter 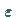 .
Das System (17.53) habe bei
.
Das System (17.53) habe bei  die hyperbolische Ruhelage
die hyperbolische Ruhelage 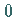 vom Sattelknoten-Typ, die für kleine
vom Sattelknoten-Typ, die für kleine 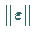 erhalten bleibe.
Die JACOBI-Matrix
erhalten bleibe.
Die JACOBI-Matrix 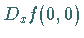 habe den Eigenwert
habe den Eigenwert 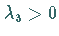 und die
konjugiert komplexen Eigenwerte
und die
konjugiert komplexen Eigenwerte 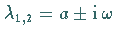 mit
mit 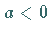 .
Weiter habe (17.53) bei
.
Weiter habe (17.53) bei  eine Separatrixschleife
eine Separatrixschleife 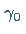 ,
d.h. einen homoklinen Orbit, der für
,
d.h. einen homoklinen Orbit, der für 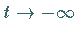 und
und 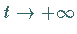 gegen
gegen 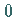 geht (s. Abbildung).
geht (s. Abbildung).
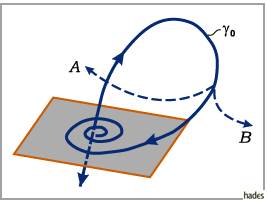
Dann hat (17.53) nahe der Separatrixschleife folgende Phasenporträts:
a) Sei 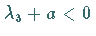 .
Bricht die Separatrixschleife bei
.
Bricht die Separatrixschleife bei 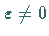 in der mit
in der mit 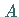 gekennzeichneten
Variante der obigen Abbildung auf, so setzt bei
gekennzeichneten
Variante der obigen Abbildung auf, so setzt bei  genau ein periodischer
Orbit von (17.53) ein.
Bricht die Separatrixschleife bei
genau ein periodischer
Orbit von (17.53) ein.
Bricht die Separatrixschleife bei 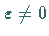 in der mit
in der mit 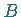 gekennzeichneten
Variante der obigen Abbildung auf, so entsteht kein periodischer Orbit.
gekennzeichneten
Variante der obigen Abbildung auf, so entsteht kein periodischer Orbit.
b) Sei 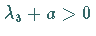 .
Dann existieren bei
.
Dann existieren bei  (bzw. für kleine
(bzw. für kleine 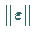 )
nahe der
Separatrixschleife
)
nahe der
Separatrixschleife 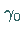 (bzw. nahe der zerfallenen Schleife
(bzw. nahe der zerfallenen Schleife 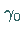 )
abzählbar unendlich viele sattelartige periodische Orbits.
Die POINCARÉ-Abbildung bezüglich einer zu
)
abzählbar unendlich viele sattelartige periodische Orbits.
Die POINCARÉ-Abbildung bezüglich einer zu 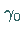 transversalen Ebene
erzeugt bei
transversalen Ebene
erzeugt bei  eine abzählbar unendliche Menge von
Hufeisen-Abbildungen, von denen bei kleinen
eine abzählbar unendliche Menge von
Hufeisen-Abbildungen, von denen bei kleinen
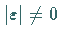 eine endliche Anzahl bleibt.
eine endliche Anzahl bleibt.