Themen dieser Seite
Prüfen mit Hilfe des Wahrscheinlichkeitspapiers
In einem rechtwinkligen Koordinatensystem ist die 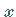 -Achse gleichabständig unterteilt,
während die
-Achse gleichabständig unterteilt,
während die 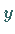 -Achse die folgende Skala darstellt:
Sie ist gleichabständig bezüglich
-Achse die folgende Skala darstellt:
Sie ist gleichabständig bezüglich 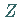 unterteilt, wird aber mit
unterteilt, wird aber mit
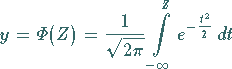 |
(16.132) |
beziffert.
Falls eine Zufallsgröße 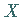 einer Normalverteilung mit Mittelwert
einer Normalverteilung mit Mittelwert 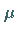 und Streuung
und Streuung
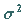 genügt, dann gilt für ihre Verteilungsfunktion
genügt, dann gilt für ihre Verteilungsfunktion
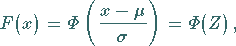 |
(16.133a) |
d.h., es muß
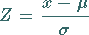 |
(16.133b) |
gelten und damit ein linearer Zusammenhang zwischen 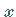 und
und 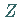 bestehen.
Aus der Substitution (16.133b) liest man außerdem die folgende
Zuordnung ab:
Entnimmt man einer normalverteilten Grundgesamtheit eine Stichprobe, berechnet deren
relative Summationshäufigkeiten gemäß (16.127) und trägt diese in das
Wahrscheinlichkeitspapier als Ordinaten zu den entsprechenden oberen Klassengrenzen als
Abszissen ein, dann liegen diese Punkte annähernd (bis auf zufällige Abweichungen)
auf einer Geraden (s. Abbildung).
bestehen.
Aus der Substitution (16.133b) liest man außerdem die folgende
Zuordnung ab:
Entnimmt man einer normalverteilten Grundgesamtheit eine Stichprobe, berechnet deren
relative Summationshäufigkeiten gemäß (16.127) und trägt diese in das
Wahrscheinlichkeitspapier als Ordinaten zu den entsprechenden oberen Klassengrenzen als
Abszissen ein, dann liegen diese Punkte annähernd (bis auf zufällige Abweichungen)
auf einer Geraden (s. Abbildung).
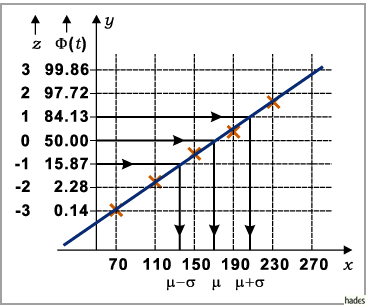
Aus der Abbildung ist ersichtlich, daß für das zu Grunde liegende Beispiel eine
Normalverteilung angenommen werden kann.
Außerdem liest man ab:
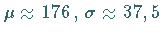 .
.
Hinweis: Die Werte 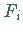 der relativen Summenhäufigkeiten lassen sich einfacher
in das Wahrscheinlichkeitspapier eintragen, wenn dessen Bezifferung der Ordinate
bezüglich
der relativen Summenhäufigkeiten lassen sich einfacher
in das Wahrscheinlichkeitspapier eintragen, wenn dessen Bezifferung der Ordinate
bezüglich 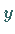 gleichabständig ist, was ungleichabständige Ordinaten zur Folge hat.
gleichabständig ist, was ungleichabständige Ordinaten zur Folge hat.
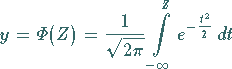
![]() der relativen Summenhäufigkeiten lassen sich einfacher
in das Wahrscheinlichkeitspapier eintragen, wenn dessen Bezifferung der Ordinate
bezüglich
der relativen Summenhäufigkeiten lassen sich einfacher
in das Wahrscheinlichkeitspapier eintragen, wenn dessen Bezifferung der Ordinate
bezüglich ![]() gleichabständig ist, was ungleichabständige Ordinaten zur Folge hat.
gleichabständig ist, was ungleichabständige Ordinaten zur Folge hat.