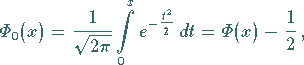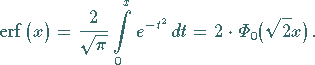Normierte Normalverteilung, Gaußsches Fehlerintegral
1. Verteilungsfunktion und Dichtefunktion:
Aus (16.69) erhält man für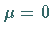 
und 
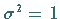die
Verteilungsfunktion
 |
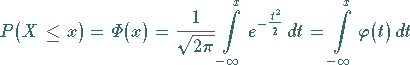(16.73a) |
der normierten Normalverteilung .
Ihre Dichtefunktion
 |
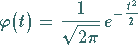(16.73b) |
beschreibt die GAUSSsche Glockenkurve (s. Abbildung).
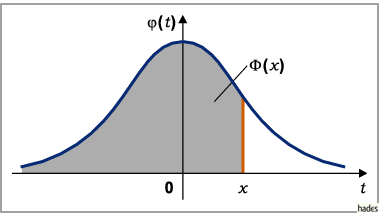
Die (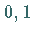
)-Normalverteilung 
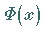liegt tabelliert vor
(Tabelle Normierte Normalverteilung), und zwar hier nur für positive
Argumente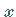 
,
da für negative Argumente der Zusammenhang
 |
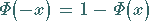(16.74) |
genutzt werden kann.
2. Wahrscheinlichkeitsintegral:
Das Integral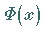
wird auch Wahrscheinlichkeitsintegral oder
GAUSSsches Fehlerintegral genannt.
In der Literatur findet man dafür auch die folgenden Definitionen:
 |
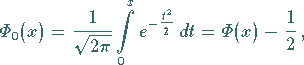(16.75a) |
 |
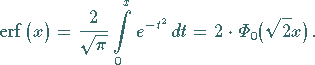(16.75b) |
(Zur Fehler-Funktion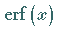 
s. auch Fehler-Funktion.)
