Summe aus linearer und gebrochenlinearer Funktion
Die konforme Abbildung
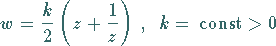 |
(14.16a) |
kann mit Hilfe der Polarkoordinatendarstellung 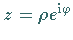 und Trennung
von Real- und Imaginärteil gemäß (14.8) zu
und Trennung
von Real- und Imaginärteil gemäß (14.8) zu
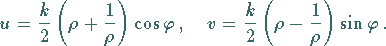 |
(14.16b) |
umgeformt werden.
Kreise mit 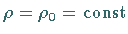 der
der 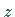 -Ebene (s. linke Abbildung) gehen in
die konfokalen Ellipsen
-Ebene (s. linke Abbildung) gehen in
die konfokalen Ellipsen
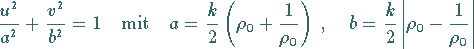 |
(14.16c) |
der 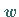 -Ebene (s. rechte Abbildung) über.
-Ebene (s. rechte Abbildung) über.
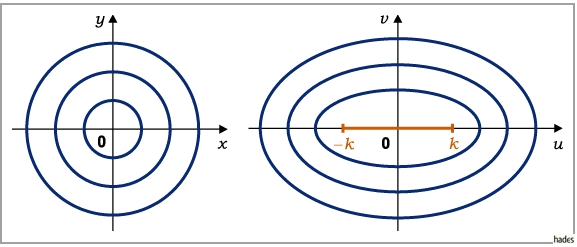
Brennpunkte sind die Punkte 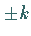 der reellen Achse.
Für den Einheitskreis mit
der reellen Achse.
Für den Einheitskreis mit 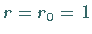 entartet die Ellipse der
entartet die Ellipse der 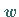 -Ebene in die
zweifach durchlaufene Strecke
-Ebene in die
zweifach durchlaufene Strecke 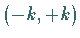 der reellen Achse.
Sowohl das Innere als auch das Äußere des Einheitskreises wird auf die volle
der reellen Achse.
Sowohl das Innere als auch das Äußere des Einheitskreises wird auf die volle
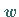 -Ebene mit dem Schnitt
-Ebene mit dem Schnitt 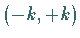 abgebildet, so daß die Umkehrfunktion zweideutig
ist:
abgebildet, so daß die Umkehrfunktion zweideutig
ist:
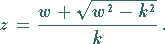 |
(14.16d) |
Die Geraden 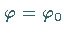 der
der 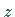 -Ebene (s. die folgende linke Abbildung) werden
in die konfokalen Hyperbeln
-Ebene (s. die folgende linke Abbildung) werden
in die konfokalen Hyperbeln
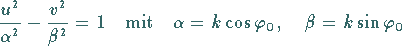 |
(14.16e) |
mit den Brennpunkten 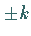 abgebildet (s. rechte Abbildung).
abgebildet (s. rechte Abbildung).
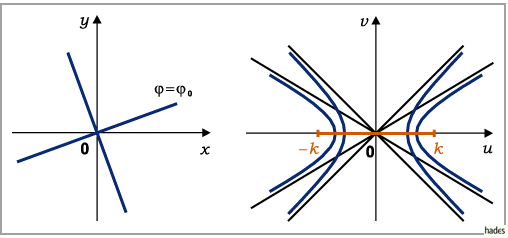
Die den Koordinatenhalbachsen der 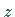 -Ebene
-Ebene
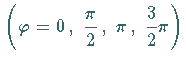 entsprechenden Hyperbeln arten in die Achse
entsprechenden Hyperbeln arten in die Achse 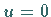 und in die hin und zurück
durchlaufenen Intervalle
und in die hin und zurück
durchlaufenen Intervalle 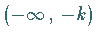 und
und 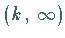 der reellen Achse aus.
der reellen Achse aus.
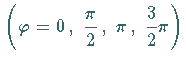 entsprechenden Hyperbeln arten in die Achse
entsprechenden Hyperbeln arten in die Achse