Unter einer konformen Abbildung versteht man die Abbildung der 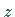 - in die
- in die 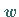 -Ebene
mit Hilfe einer analytischen Funktion
-Ebene
mit Hilfe einer analytischen Funktion 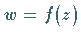 in allen Punkten
in allen Punkten 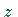 ,
in denen
,
in denen
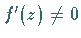 ist.
ist.
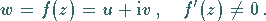 |
(14.8) |
Die konforme Abbildung besitzt die folgende Haupteigenschaft:
Alle Linienelemente 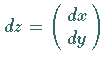 im Punkt
im Punkt 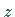 erfahren bei der
Überführung in Linienelemente
erfahren bei der
Überführung in Linienelemente 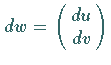 im Punkt
im Punkt 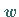 dieselbe
Streckung im Verhältnis
dieselbe
Streckung im Verhältnis 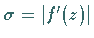 und dieselbe Drehung um den Winkel
und dieselbe Drehung um den Winkel
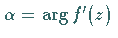 .
Dadurch werden geometrische Gebilde in einem infinitesimalen Gebiet in ähnliche Figuren
transformiert, behalten also ihre Form bei (s. Abbildung):
.
Dadurch werden geometrische Gebilde in einem infinitesimalen Gebiet in ähnliche Figuren
transformiert, behalten also ihre Form bei (s. Abbildung):
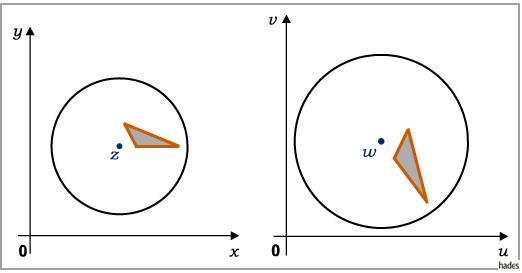
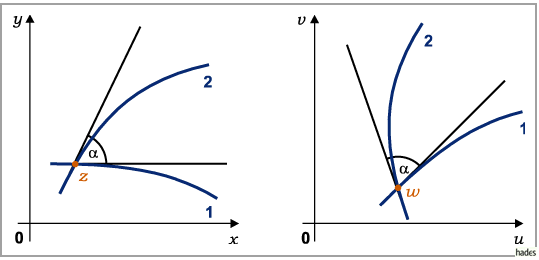
Geometrische Gebilde endlicher Abmessungen werden zwar verzerrt dargestellt, die
Schnittwinkel zwischen den Kurven bleiben aber erhalten, u.a. auch die Orthogonalität
der Kurvenscharen (s. Abbildung).
Konforme Abbildungen haben in der Physik, Elektrotechnik, Hydro- und Aerodynamik sowie in
anderen Anwendungsgebieten der Mathematik weite Verbreitung gefunden.
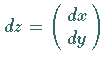 im Punkt
im Punkt 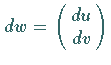 im Punkt
im Punkt