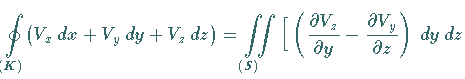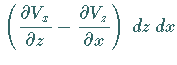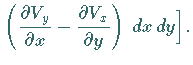Integralsatz von Stokes
Der Integralsatz von STOKES liefert den Zusammenhang zwischen einem
Oberflächenintegral über die gekrümmte und orientierte Fläche 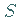 ,
in der das
Vektorfeld
,
in der das
Vektorfeld 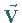 definiert ist, und dem Umlaufintegral über die Umrandungskurve
definiert ist, und dem Umlaufintegral über die Umrandungskurve
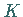 der Fläche
der Fläche 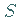 .
Der Umlaufsinn von
.
Der Umlaufsinn von 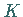 wird so gewählt, daß der Umlaufsinn der Berandung des
Oberflächenelements mit der Flächennormalen eine Rechtsschraube
bildet.
Die vektorielle Feldfunktion
wird so gewählt, daß der Umlaufsinn der Berandung des
Oberflächenelements mit der Flächennormalen eine Rechtsschraube
bildet.
Die vektorielle Feldfunktion 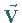 sei stetig und besitze stetige partielle
Ableitungen 1. Ordnung.
sei stetig und besitze stetige partielle
Ableitungen 1. Ordnung.
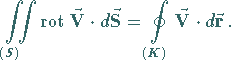 |
(13.120a) |
Der vektorielle Fluß der Rotation durch eine Fläche 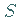 ,
die von der geschlossenen
Kurve
,
die von der geschlossenen
Kurve 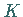 umrandet wird, ist gleich dem Umlaufintegral des vektoriellen Feldes
umrandet wird, ist gleich dem Umlaufintegral des vektoriellen Feldes
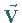 über die Kurve
über die Kurve 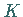 .
.
In kartesischen Koordinaten gilt:
Im ebenen Falle geht der Integralsatz von STOKES ebenso wie der von GAUSS
in die Integralformel (13.118) von GAUSS über.
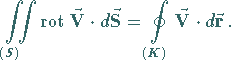
![]() ,
die von der geschlossenen
Kurve
,
die von der geschlossenen
Kurve ![]() umrandet wird, ist gleich dem Umlaufintegral des vektoriellen Feldes
umrandet wird, ist gleich dem Umlaufintegral des vektoriellen Feldes
![]() über die Kurve
über die Kurve ![]() .
.