|
|
|
|
 |
(13.121) |
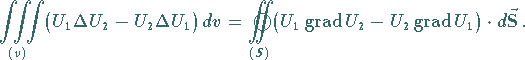 |
(13.122) |
Speziell für ![]() gilt:
gilt:
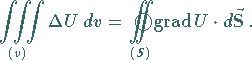 |
(13.123) |
In kartesischen Koordinaten hat der 3. GREENsche Satz die folgende Form:
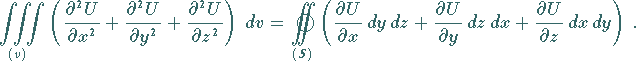 |
(13.124) |
| Beispiel A | |
|
Berechnung des Linienintegrals:
| |
| Beispiel B | |
|
Gesucht ist der Fluß | |
| Beispiel C | |
|
Wärmeleitungsgleichung: Die zeitliche Änderung des Wärmeinhaltes | |
|
|
|