Vektor eines ebenen Flächenstückes
Die vektorielle Darstellung des
Oberflächenintegrals zweiter Gattung allgemeiner Art erfordert die
Zuordnung eines Vektors 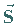 zu einem Flächenstück
zu einem Flächenstück 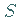 ,
der senkrecht auf
dieser Fläche steht und dessen Betrag gleich dem Flächeninhalt von
,
der senkrecht auf
dieser Fläche steht und dessen Betrag gleich dem Flächeninhalt von 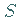 ist.
Den Fall eines ebenen Flächenstückes zeigt die folgende Abbildung.
ist.
Den Fall eines ebenen Flächenstückes zeigt die folgende Abbildung.
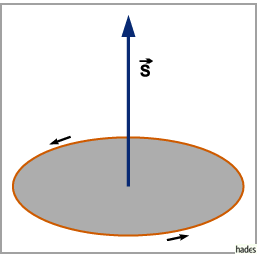
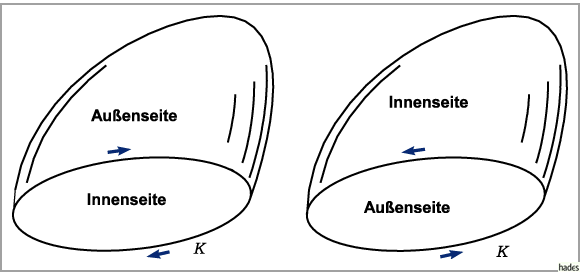
Die positive Richtung von 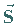 wird gemäß der Rechte-Hand-Regel (auch
Rechtsschraube genannt) mit dem der geschlossenen Umrandungskurve
wird gemäß der Rechte-Hand-Regel (auch
Rechtsschraube genannt) mit dem der geschlossenen Umrandungskurve  bei gegebenen
Umlaufsinn festgelegt:
Blickt man vom Vektorursprung in Richtung Vektorspitze, dann soll der
Drehsinn der Umrandungskurve mit dem des Uhrzeigers übereinstimmen.
Durch diese Wahl des positiven Umlaufsinnes auf der Umrandungskurve wird gleichzeitig
festgelegt, welche Fläche die Außenseite ist, d.h. die Seite, von der aus der
Vektor abgetragen wird.
Diese Festlegungen können auf beliebig gekrümmte Flächenstücke übertragen
werden, die von einer geschlossenen Randkurve begrenzt werden (s. Abbildung).
bei gegebenen
Umlaufsinn festgelegt:
Blickt man vom Vektorursprung in Richtung Vektorspitze, dann soll der
Drehsinn der Umrandungskurve mit dem des Uhrzeigers übereinstimmen.
Durch diese Wahl des positiven Umlaufsinnes auf der Umrandungskurve wird gleichzeitig
festgelegt, welche Fläche die Außenseite ist, d.h. die Seite, von der aus der
Vektor abgetragen wird.
Diese Festlegungen können auf beliebig gekrümmte Flächenstücke übertragen
werden, die von einer geschlossenen Randkurve begrenzt werden (s. Abbildung).