Berechnung von Oberflächenintegralen
Die Berechnung von Oberflächenintegralen in Skalar- oder Vektorfeldern kann unabhängig
davon, ob 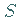 von einer geschlossenen Kurve umrandet ist oder selbst eine geschlossene
Fläche darstellt, in fünf Schritten erfolgen:
von einer geschlossenen Kurve umrandet ist oder selbst eine geschlossene
Fläche darstellt, in fünf Schritten erfolgen:
1. Einteilung des Flächenstückes 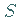 ,
auf dem die Außenseite durch den
Umlaufsinn der Randkurve bestimmt ist (s. Abbildung), in beliebige
,
auf dem die Außenseite durch den
Umlaufsinn der Randkurve bestimmt ist (s. Abbildung), in beliebige 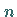 Teilflächenstücke
Teilflächenstücke 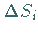 derart, daß jedes dieser Teilflächenstücke
durch ein ebenes Flächenstück angenähert werden kann.
Jedem Flächenstück
derart, daß jedes dieser Teilflächenstücke
durch ein ebenes Flächenstück angenähert werden kann.
Jedem Flächenstück 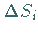 wird gemäß (13.31a) der
Vektor
wird gemäß (13.31a) der
Vektor 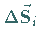 zugeordnet
zugeordnet
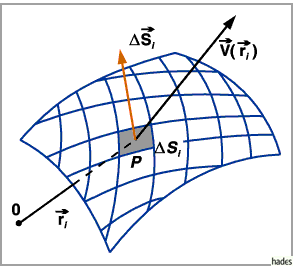
Im Falle einer geschlossenen Fläche wird der positive Umlaufsinn der Randkurve so
festgelegt, daß die positive Seite, auf der der Vektor 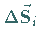 beginnt,
die Außenfläche ist.
beginnt,
die Außenfläche ist.
2. Auswahl eines beliebigen Punktes mit dem Ortsvektor 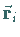 im Innern
oder auf dem Rande jedes Teilflächenstückes.
im Innern
oder auf dem Rande jedes Teilflächenstückes.
3. Bildung des Produktes 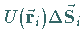 im Falle des skalaren
Feldes und
im Falle des skalaren
Feldes und 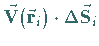 oder
oder
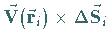 im Falle eines vektoriellen Feldes.
im Falle eines vektoriellen Feldes.
4. Addition der für die Teilflächenstücke gebildeten Produkte.
5. Bildung des Grenzüberganges 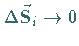 für
für 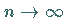 .
Dabei sollen die Teilflächenstücke in dem bei der Berechnung des Doppelintegrals
angegebenen Sinne gegen Null streben.
.
Dabei sollen die Teilflächenstücke in dem bei der Berechnung des Doppelintegrals
angegebenen Sinne gegen Null streben.