Definition der Divergenz
Zu einem Vektorfeld 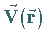 läßt sich ein skalares Feld, das
Feld seiner Divergenz , angeben.
Im Punkt
läßt sich ein skalares Feld, das
Feld seiner Divergenz , angeben.
Im Punkt  ist die Divergenz als Volumenableitung des Vektorfeldes definiert:
ist die Divergenz als Volumenableitung des Vektorfeldes definiert:
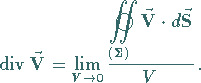 |
(13.46) |
Man bezeichnet die Divergenz eines Vektorfeldes auch als spezifische Ergiebigkeit oder
Quelldichte, denn sie gibt, falls 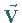 ein Strömungsfeld beschreibt, die
Flüssigkeitsmenge an, die in dem betreffenden Punkt des Feldes
ein Strömungsfeld beschreibt, die
Flüssigkeitsmenge an, die in dem betreffenden Punkt des Feldes 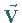 je
Volumen- und Zeiteinheit neu entsteht.
Im Fall
je
Volumen- und Zeiteinheit neu entsteht.
Im Fall 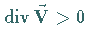 spricht man vom Vorhandensein einer Quelle ,
im Fall
spricht man vom Vorhandensein einer Quelle ,
im Fall 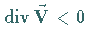 vom Vorhandensein einer Senke .
vom Vorhandensein einer Senke .