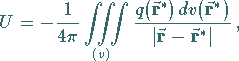Poissonsche Differentialgleichung
Die Aufgabe der Bestimmung des Potentials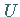 
eines Vektorfeldes
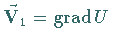in dem Quellen enthalten sind, führt gemäß
(13.127a) mit 
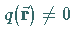auf
 |
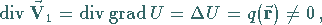(13.131a) |
d.h. auf die POISSONsche Differentialgleichung .
In kartesischen Koordinaten gilt:
 |
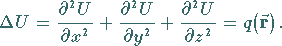(13.131b) |
Die LAPLACEsche Differentiagleichung (13.130b) ist somit ein Spezialfall der
POISSONschen Differentialgleichung (13.131b).
Lösungen sind das NEWTON-Potential (für Punktmassen) oder das
COULOMB-Potential (für Punktladungen)
 |
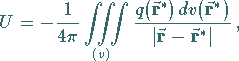(13.131c) |
deren Potential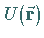 
für betragsmäßig größer werdende
-Werte hinreichend stark gegen Null strebt.
Zur POISSONschen Differentialgleichung können die gleichen drei
Randwertbedingungen wie für die Lösung der LAPLACEschen Differentialgleichung
formuliert werden. Die erste und dritte Randwertaufgabe sind eindeutig lösbar, an die
zweite müssen noch spezielle Bedingungen gestellt werden (s. Lit. 9.6).
