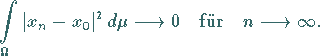Konvergenz von Folgen im metrischen Raum
Seien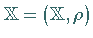 
ein metrischer Raum, 
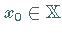ein Punkt und
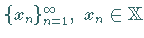eine Folge von Elementen in 
.
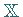Die Folge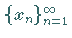 
heißt zum Punkt 
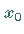konvergent, wenn es zu
jeder Umgebung 
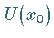einen Index 
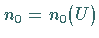gibt, so daß 
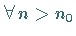die Beziehung 
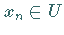gilt.
Man schreibt für diesen Sachverhalt gewöhnlich
 |
(12.51) |
und nennt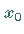
den Grenzwert der Folge 
.
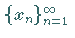Der Grenzwert einer Folge ist eindeutig bestimmt.
Anstelle einer beliebigen (allgemeinen) Umgebung des Punktes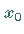
genügt es,
lediglich offene Kugeln mit beliebig kleinem Radius heranzuziehen, so daß
(12.51) äquivalent zu Folgendem ist:
Für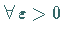 
(man hat dabei sofort die offene Kugel
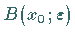im Sinn) gibt es einen Index 
,
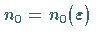so
daß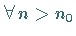
die Ungleichung 
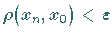gilt.
Damit bedeutet (12.51) genau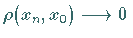 
.
Mit den eingeführten Begriffen hat man die Möglichkeit, in konkreten metrischen
Räumen den Abstand zwischen zwei Punkten anzugeben und die Konvergenz von Punktfolgen
zu untersuchen, was etwa bei numerischen Verfahren oder bei der Approximation von
Funktionen durch solche einer bestimmten Klasse (s. etwa
Approximation und Ausgleichsrechnung) von Bedeutung
ist.
Im Raum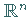 
erweist sich die mittels einer der angegebenen Metriken festgelegte
Konvergenz gerade als die koordinatenweise Konvergenz.
In den Räumen 
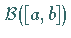und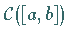 
ist die durch (12.45)
eingeführte Konvergenz genau die gleichmäßige Konvergenz der
Funktionenfolge auf der Menge 
.
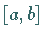Im Raum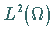 
ergibt sich die Konvergenz im (quadratischen) Mittel, d.h.
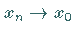genau dann, wenn
 |
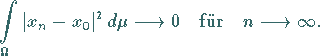(12.52) |
