Einige Eigenschaften des Integrals
Sei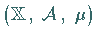 
ein Maßraum und seien
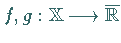meßbare Funktionen und
.
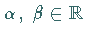1. Ist 
integrierbar, dann ist
fast überall endlich, d.h.
.
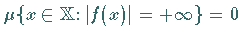2. Ist
integrierbar, dann gilt
.
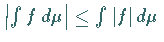3. Ist
integrierbar und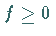 
,
dann gilt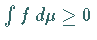 
.
4. Ist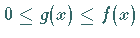 
auf 
und
integrierbar, dann ist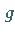 
integrierbar, und es gilt 
.
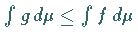5. Sind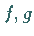 
integrierbar, dann ist 
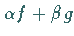integrierbar, und es
gilt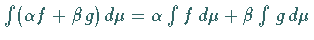 
.
6. Sind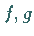
integrierbar auf 
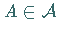mit
,
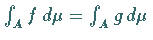dann gilt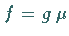 
-f.ü. auf 
.
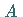Ist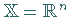 
und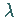 
das LEBESGUE-Maß, dann spricht man vom
(
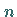-dimensionalen) LEBESGUE-Integral .
Im Falle 
und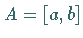 
ist für jede stetige Funktion
auf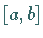 
sowohl das
RIEMANN-Integral 
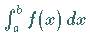als auch
das LEBESGUE-Integral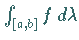 
definiert.
Beide Werte sind endlich und stimmen überein.
Mehr noch, ist
eine auf
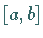beschränkte RIEMANN-integrierbare Funktion,
dann ist sie auch LEBESGUE-integrierbar (integrierbar im LEBESGUEschen Sinne),
wobei die Werte beider Integrale identisch sind (Natürlichkeit des
LEBESGUE-Integrals).
Die Menge der LEBESGUE-integrierbaren Funktionen ist aber wesentlich
umfassender und besitzt eine Reihe von Vorteilen, die sich insbesondere bei
Grenzübergängen unter dem Integral zeigen.
