Bestimmtes Integral als Grenzwert einer Summe
Der Grenzwert, der zum bestimmten Integral führt, wird wie folgt gebildet
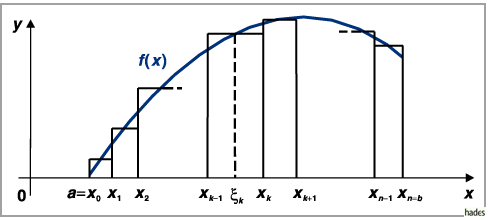
(s. Abbildung)
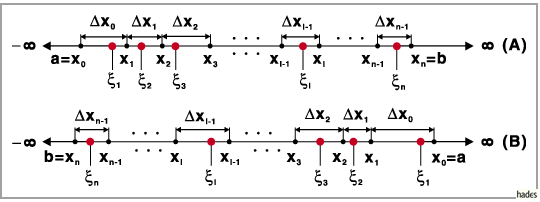
1. Schritt: Das Intervall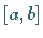 
wird durch 
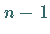beliebige Teilpunkte
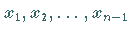in 
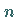,,Elementarintervalle`` zerlegt, die so gewählt sind,
daß einer der folgenden Fälle gilt:
 |
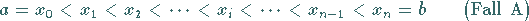(8.35a) |
oder
 |
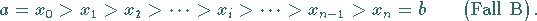(8.35b) |
2. Schritt: Im Innern oder auf dem Rande jedes der Elementarintervalle wird
in Übereinstimmung mit der Abbildung eine Zahl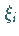 
ausgewählt:
 |
(8.35c) |
3. Schritt: Die Werte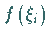 
der Funktion 
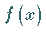in diesen
ausgewählten Punkten werden mit der zugehörigen Differenz
,
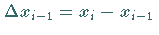d.h. mit den Längen der Teilintervalle multipliziert,
die im Falle A mit positivem Vorzeichen, im Falle B mit negativem Vorzeichen zu nehmen
sind.
Auf diese Weise entsteht für den Fall A das Bild der Abbildung, die bereits bei der
Einführung des Begriffs ,,bestimmtes Integral``
betrachtet wurde:
4. Schritt: Alle so gewonnenen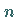
Produkte 
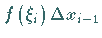werden addiert.
5. Schritt: Von der auf diese Weise entstehenden Zerlegungs- oder Zwischensumme
 |
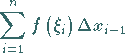(8.36) |
wird der Grenzwert für den Fall berechnet, daß die Länge der Elementarintervalle
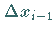gegen Null strebt und demzufolge ihre Anzahl gegen 
.
Auf Grund dieser Eigenschaft wird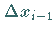
auch als infinitesimale Größe
bezeichnet.
Wenn dieser Grenzwert existiert und unabhängig ist von der Wahl der Zahlen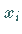 
und
,
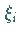heißt er das bestimmte RIEMANNsche Integral der betreffenden
Funktion in dem gegebenen Intervall.
Man schreibt dafür
 |
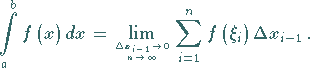(8.37) |
Die beiden Intervallgrenzen werden zu Integrationsgrenzen ; sie legen das
Integrationsintervall fest.
Man nennt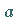 
die untere , 
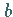die obere Integrationsgrenze ;
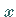heißt Integrationsvariable , 
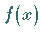Integrand .
