Leray-Schauder-Theorie
Für die Existenz von Lösungen der Gleichungen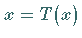 
und 
,
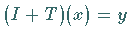mit
jeweils vollstetigem Operator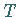 
,
ist auf der Grundlage tiefliegender Eigenschaften
des Abbildungsgrades ein weiteres Prinzip entdeckt worden, das etwa für Existenzbeweise
bei nichtlinearen Randwertproblemen erfolgreich eingesetzt wird.
Die hier angeführten Resultate dieser Theorie sind für praktische Belange vielfach
die geeignetsten, wobei Formulierungen gewählt wurden, die ohne Erwähnung des
Abbildungsgrades auskommen.
Satz von Leray-Schauder, 1. Formulierung: Seien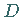 
eine offene
beschränkte Menge eines rellen BANACH-Raumes 
und
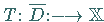ein vollstetiger
Operator.
Sei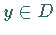 
ein solcher Punkt, daß 
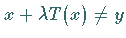für alle
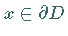und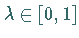 
gilt, wobei 
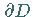den Rand der Menge
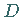bezeichnet.
Dann hat die Gleichung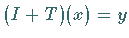 
wenigstens eine Lösung.
Satz von Leray-Schauder, 2. Formulierung: In Anwendungen erweist sich
häufig auch die folgende Variante dieses Satzes als vorteilhaft.
Sei 
ein vollstetiger Operator auf dem BANACH-Raum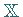 
.
Wenn die Lösungen der Gleichungsschar
 |
(12.197) |
eine gleichmäßige apriori -Abschätzung gestatten, d. h.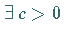 
,
so daß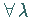 
und 
,
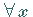die (12.197) genügen, die
Ungleichung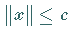 
gilt, dann besitzt die Gleichung
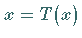eine Lösung.
