Seien 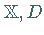 wie im vorhergehenden Abschnitt und
wie im vorhergehenden Abschnitt und
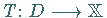 .
Unter der Voraussetzung der Differenzierbarkeit von
.
Unter der Voraussetzung der Differenzierbarkeit von  in jedem Punkt der Menge
in jedem Punkt der Menge 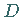 ist
ein Operator
ist
ein Operator 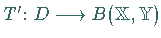 definiert, der jedem
definiert, der jedem
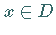 das Element
das Element 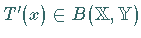 zuordnet.
Der Operator
zuordnet.
Der Operator 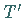 sei auf
sei auf 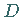 stetig (in der Operatornorm); in diesem Falle sagt man,
stetig (in der Operatornorm); in diesem Falle sagt man,
 ist stetig differenzierbar auf
ist stetig differenzierbar auf 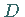 .
Die Menge
.
Die Menge 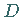 enthalte eine Lösung
enthalte eine Lösung 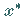 der Gleichung
der Gleichung
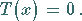 |
(12.194) |
Weiter sei vorausgesetzt, daß für 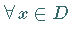 der Operator
der Operator 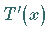 stetig invertierbar ist, also
stetig invertierbar ist, also 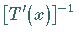 in
in 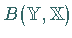 liegt.
Für ein beliebiges Element
liegt.
Für ein beliebiges Element 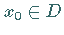 vermutet man wegen (12.192), daß die
Elemente
vermutet man wegen (12.192), daß die
Elemente 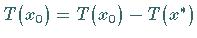 und
und 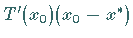 ,,nahe``
beieinander liegen und demzufolge die Lösung der linearen Gleichung, also (unter
den gemachten Voraussetzungen)
,,nahe``
beieinander liegen und demzufolge die Lösung der linearen Gleichung, also (unter
den gemachten Voraussetzungen)
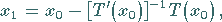 |
(12.195) |
das gesuchte Element 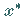 approximiert.
Auf diese Weise konstruiert man, ausgehend von
approximiert.
Auf diese Weise konstruiert man, ausgehend von 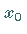 ,
die sogenannte
NEWTON sche Näherungsfolge
,
die sogenannte
NEWTON sche Näherungsfolge
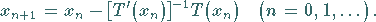 |
(12.196) |
Die Begründung für das beschriebene Vorgehen wird durch eine Reihe von Sätzen,
die sich im Allgemeinheitsgrad oder in der Anpassung an spezielle Situationen der
gemachten Voraussetzungen unterscheiden, geliefert, von denen exemplarisch nur der
folgende zitiert werden soll, aus dem die wesentlichen Eigenschaften und Vorteile des
Verfahrens erkennbar werden:
Es gibt zu 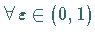 eine Kugel
eine Kugel
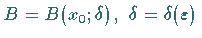 ,
so daß alle
,
so daß alle 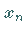 in
in 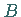 liegen und die NEWTONsche Folge zur Lösung
liegen und die NEWTONsche Folge zur Lösung 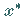 von (12.194) konvergiert.
Darüber hinaus gilt
von (12.194) konvergiert.
Darüber hinaus gilt 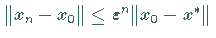 .
.
Das modifizierte NEWTON-Verfahren erhält man, wenn man in der Formel
(12.196) stets den Operator 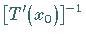 anstelle von
anstelle von
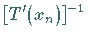 benutzt.
Für weitere Abschätzungen der Konvergenzgeschwindigkeit, und zur (im allgemeinen
sensiblen) Abhängigkeit des Verfahrens vom Startpunkt
benutzt.
Für weitere Abschätzungen der Konvergenzgeschwindigkeit, und zur (im allgemeinen
sensiblen) Abhängigkeit des Verfahrens vom Startpunkt 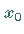 s. Lit. 12.7, 12.13, 12.15,
12.21.
s. Lit. 12.7, 12.13, 12.15,
12.21.
![]() anstelle von
anstelle von
![]() benutzt.
Für weitere Abschätzungen der Konvergenzgeschwindigkeit, und zur (im allgemeinen
sensiblen) Abhängigkeit des Verfahrens vom Startpunkt
benutzt.
Für weitere Abschätzungen der Konvergenzgeschwindigkeit, und zur (im allgemeinen
sensiblen) Abhängigkeit des Verfahrens vom Startpunkt ![]() s. Lit. 12.7, 12.13, 12.15,
12.21.
s. Lit. 12.7, 12.13, 12.15,
12.21.