Differenzierbarkeit nichtlinearer Operatoren
Seien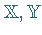 
BANACH-Räume, 
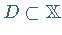eine offene Menge und
.
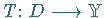Der Operator 
heißt FRÉCHET- differenzierbar im Punkt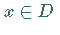 
,
wenn ein (im allgemeinen von der Stelle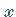 
abhängiger, linearer stetiger) Operator
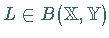existiert, so daß
 |
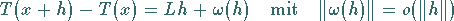(12.192) |
oder in äquivalenter Schreibweise
 |
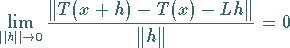(12.193) |
gilt, d.h.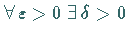 
,
so daß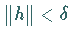 
die Ungleichung 
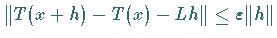impliziert.
Der Operator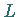 
,
den man gewöhnlich mit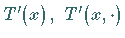 
oder
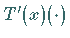bezeichnet, heißt FRÉCHET-Ableitung des Operators
im Punkt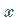 
.
Den Wert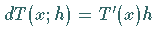 
nennt man FRÉCHET- Differential des
Operators
im Punkt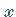
(für den Zuwachs 
).
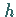In jedem Falle ist die Abhängigkeit des Operators von der Stelle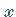
erkennbar, die
letzteren Bezeichnungen ,,weisen den Platz für das Argument aus``, auf das der
Operator angewendet werden kann.
Aus der Differenzierbarkeit eines Operators in einem Punkt folgt seine Stetigkeit in
diesem Punkt.
Ist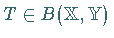 
,
also selbst bereits linear und stetig, dann ist
in jedem Punkt
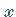differenzierbar, und die Ableitung ist gleich 
.
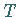