Sei 
ein kompakter linearer Operator in einem BANACH-Raum 
.
Es werden die folgenden Gleichungen zweiter Art mit einem Parameter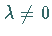 
betrachtet:
 |
(12.185a) |
 |
(12.185b) |
Es gelten:
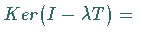1. dim
dim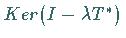
,
d.h., die homogenen
Gleichungen haben stets dieselbe endliche Anzahl von linear unabhängigen Lösungen.
2. 
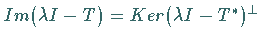und
.
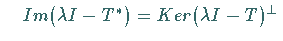(Hier ist die Orthogonalität im BANACH-Raum gemeint.)
3. 
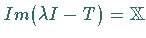genau dann, wenn 
.
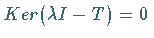4. Die FREDHOLMsche Alternative (auch RIESZ-SCHAUDER-Theorie
genannt), d.h. entweder:
a) Die homogene Gleichung besitzt nur die triviale Lösung.
In diesem Falle gilt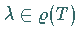 
,
der Operator 
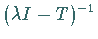ist
beschränkt, und die inhomogene Gleichung besitzt genau eine Lösung
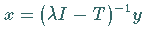für beliebiges 
,
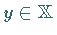oder:
b) Die homogene Gleichung besitzt wenigstens eine nichttriviale Lösung.
In diesem Falle gilt: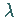 
ist ein Eigenwert von 
,
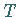also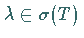 
,
und die inhomogene Gleichung besitzt eine (nicht eindeutige) Lösung genau dann, wenn
die rechte Seite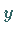 
der Bedingung 
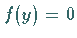für jede Lösung 
der adjungierten
Gleichung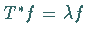 
genügt.
In letzterem Fall erhält man jede Lösung der inhomogenen Gleichung in der Form
,
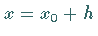wobei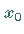 
eine feste Lösung der inhomogenen Gleichung und
ist.
Lineare Gleichungen der Gestalt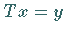 
mit kompaktem Operator
nennt man von erster Art.
Ihre Behandlung ist im allgemeinen etwas schwieriger (s. Lit. 12.12,
12.21).
