Stetige lineare Funktionale im Hilbert-Raum, Satz von Riesz
Im HILBERT-Raum  definiert jedes Element
definiert jedes Element 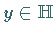 mittels
mittels 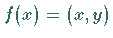 ein
lineares stetiges Funktional mit der Norm
ein
lineares stetiges Funktional mit der Norm 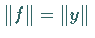 .
Andererseits, ist
.
Andererseits, ist  ein lineares stetiges Funktional auf
ein lineares stetiges Funktional auf  ,
dann existiert genau
ein Element
,
dann existiert genau
ein Element 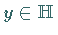 ,
so daß gilt:
,
so daß gilt:
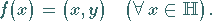 |
(12.160) |
Die Räume  und
und  sind nach diesem Satz isomorph, weshalb man sie
identifiziert.
sind nach diesem Satz isomorph, weshalb man sie
identifiziert.
Der Satz von RIESZ enthält einen Hinweis darauf, wie man die Orthogonalität
in einem beliebigen normierten Raum einführen kann.
Seien 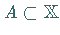 und
und 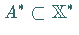 .
Dann nennt man die Mengen
.
Dann nennt man die Mengen
 |
(12.161) |
jeweils das orthogonale Komplement oder den Annulator zu  bzw.
bzw. 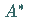 .
.
![]() und
und ![]() .
Dann nennt man die Mengen
.
Dann nennt man die Mengen