Sei 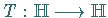 ein kompakter Operator.
Dann ist
ein kompakter Operator.
Dann ist  Grenzwert (in
Grenzwert (in 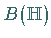 )
einer Folge von endlichdimensionalen Operatoren.
Die Nähe zum endlichdimensionalen Fall ersieht man unter anderem aus folgendem:
)
einer Folge von endlichdimensionalen Operatoren.
Die Nähe zum endlichdimensionalen Fall ersieht man unter anderem aus folgendem:
- Ist
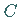 ein endlichdimensionaler Operator und
ein endlichdimensionaler Operator und 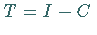 ,
dann folgt aus der
Injektivität von
,
dann folgt aus der
Injektivität von  die Existenz von
die Existenz von 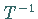 und
und 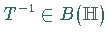 .
.
- Ist
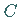 ein kompakter Operator, dann sind äquivalent:
ein kompakter Operator, dann sind äquivalent:
1. es 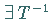 und ist stetig,
und ist stetig,
2. 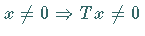 ,
d.h.
,
d.h.  ist injektiv,
ist injektiv,
3. 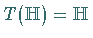 ,
d.h.
,
d.h.  ist surjektiv.
ist surjektiv.