Projektoren im Hilbert-Raum
Sei  ein Teilraum eines HILBERT-Raums
ein Teilraum eines HILBERT-Raums  .
Dann ist nach dem Projektionssatz für jedes
.
Dann ist nach dem Projektionssatz für jedes 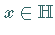 seine
Projektion
seine
Projektion 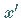 auf
auf  und demzufolge ein Operator
und demzufolge ein Operator 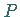 mit
mit 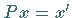 von
von  auf
auf
 definiert.
definiert.
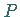 heißt Projektor auf
heißt Projektor auf  .
Offensichtlich ist
.
Offensichtlich ist 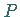 linear, stetig, und es gilt
linear, stetig, und es gilt 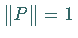 .
Ein stetiger linearer Operator
.
Ein stetiger linearer Operator 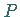 in
in  ist genau dann ein Projektor (auf einen
geeigneten Unterrraum), wenn gilt:
ist genau dann ein Projektor (auf einen
geeigneten Unterrraum), wenn gilt:
a) 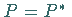 ,
d.h.
,
d.h. 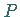 ist selbstadjungiert, und
ist selbstadjungiert, und
b) 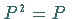 ,
d.h.
,
d.h. 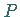 ist idempotent .
ist idempotent .