Positiv definite Operatoren
In der Menge aller selbstadjungierten Operatoren aus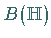 
kann durch
 |
(12.182) |
eine partielle Ordnung eingeführt werden, wobei ein Operator 
mit 
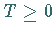positiv (definit) heißt.
Für einen selbstadjungierten Operator
gilt (mit Hilfe von 
aus
HILBERT-Raum, Skalarprodukt)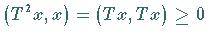 
,
so
daß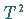 
positiv definit ist.
Jeder positiv definite Operator
besitzt seine Wurzel, d.h., es existiert genau ein
positiv definiter Operator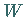 
mit 
.
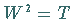Darüber hinaus ist der Vektorraum der selbstadjungierten Operatoren ein
Vektorverband, wobei die Operatoren
 |
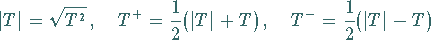(12.183) |
für die Spektralzerlegung und Spektral- bzw. Integraldarstellung von selbstadjungierten
Operatoren mit Hilfe eines STIELTJES-Integrals Bedeutung erlangen
(s. Lit. 12.1, 12.12, 12.13,
12.15, 12.18, 12.21).
