Skalarprodukt
Ein Vektorraum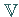 
über dem Körper 
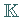(meistens wird 
betrachtet) heißt
Raum mit Skalarprodukt oder Innenproduktraum oder
Prä- HILBERT-Raum ,
wenn jedem Paar von Elementen 
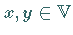eine Zahl 
,
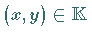das
Skalarprodukt von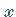 
und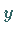 
,
zugeordnet ist, so daß für beliebige Elemente
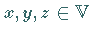und beliebiges 
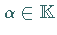die folgenden Bedingungen, die
Axiome des Skalarprodukts , erfüllt sind:
 |
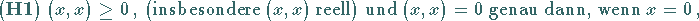(12.101) |
 |
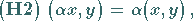(12.102) |
 |
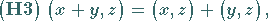(12.103) |
 |
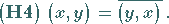(12.104) |
Hier bedeutet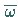 
die zu 
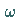konjugiert komplexe Zahl (in
(1.137b) wurde diese mit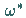 
bezeichnet).
Im Falle von 
,
also eines reellen Vektorraums, ist 
einfach
die Kommutativitätsforderung für das Skalarprodukt.
Aus den Axiomen ergeben sich sofort zusätzlich noch die Eigenschaften
 |
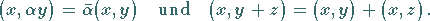(12.105) |
