|
Gegeben ist die charakteristische Integralgleichung mit konstanten Koeffizienten 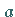 und
und
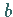
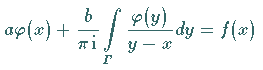 . .
Hier ist 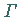 eine einfache, geschlossene Kurve, d.h.
eine einfache, geschlossene Kurve, d.h.
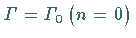 . .
Aus (11.83b) folgt 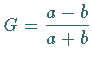 und
und
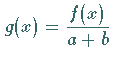 . .
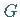 ist eine Konstante, und folglich ist
ist eine Konstante, und folglich ist  .
Somit ist .
Somit ist 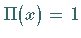 und
und
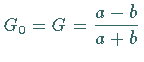 . .
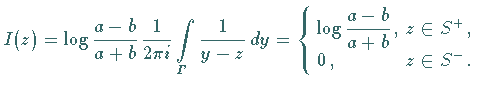
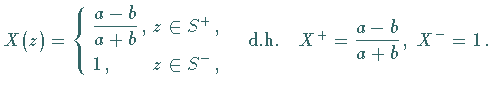
Da  ist, besitzt das homogene HILBERTsche Randwertproblem nur
ist, besitzt das homogene HILBERTsche Randwertproblem nur
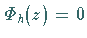 als im Unendlichen verschwindende Lösung.
Gemäß der Lösungsdarstellung (11.90) folgt
als im Unendlichen verschwindende Lösung.
Gemäß der Lösungsdarstellung (11.90) folgt
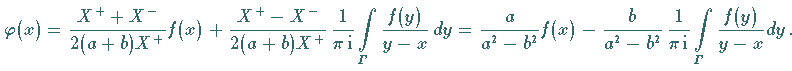
|