Die Funktion
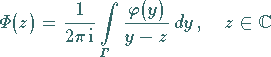 |
(11.82a) |
heißt CAUCHY-Integral über 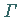 .
Für
.
Für 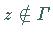 existiert das Integral im gewöhnlichen Sinne und stellt
eine holomorphe Funktion dar.
Es gilt
existiert das Integral im gewöhnlichen Sinne und stellt
eine holomorphe Funktion dar.
Es gilt 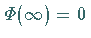 .
Für
.
Für 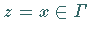 sei unter (11.82a)
der CAUCHYsche Hauptwert
sei unter (11.82a)
der CAUCHYsche Hauptwert
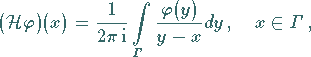 |
(11.82b) |
verstanden.
Das CAUCHY-Integral 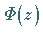 ist von
ist von 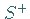 bzw.
bzw. 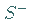 stetig auf
stetig auf 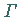 fortsetzbar.
Die Grenzwerte bei Annäherung von
fortsetzbar.
Die Grenzwerte bei Annäherung von 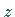 an
an 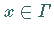 werden mit
werden mit
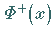 bzw.
bzw. 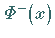 bezeichnet.
Es gelten die Formeln von PLEMELJ und SOCHOZKI:
bezeichnet.
Es gelten die Formeln von PLEMELJ und SOCHOZKI:
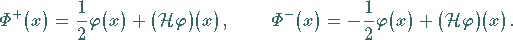 |
(11.82c) |