|
Was kann über die Wurzeln der Gleichung 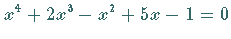 ausgesagt werden?
ausgesagt werden?
Die Koeffizienten der Gleichung haben nacheinander die Vorzeichen
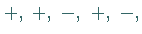 d.h., das Vorzeichen wechselt dreimal.
d.h., das Vorzeichen wechselt dreimal.
Die Gleichung besitzt in Übereinstimmung mit der Regel von DESCARTES entweder
eine oder drei positive Wurzeln.
Da beim Ersetzen von 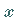 durch
durch 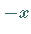 die Wurzeln der Gleichung ihre Vorzeichen ändern,
sich aber bei der Substitution von
die Wurzeln der Gleichung ihre Vorzeichen ändern,
sich aber bei der Substitution von 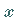 durch
durch 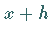 um
um 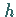 verringern, kann gemäß
der Regel von DESCARTES auch die Anzahl der negativen Wurzeln sowie die Anzahl der
Wurzeln, die größer sind als
verringern, kann gemäß
der Regel von DESCARTES auch die Anzahl der negativen Wurzeln sowie die Anzahl der
Wurzeln, die größer sind als 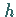 ,
abgeschätzt werden. ,
abgeschätzt werden.
Im vorliegenden Beispiel führt das Ersetzen von 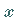 durch
durch 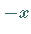 auf die Gleichung
auf die Gleichung
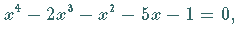 d.h., die Gleichung besitzt eine negative Wurzel.
Substituiert man
d.h., die Gleichung besitzt eine negative Wurzel.
Substituiert man 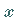 durch
durch 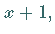 dann ergibt sich
dann ergibt sich 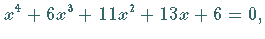 d.h., alle positiven Wurzeln der Gleichung (eine oder drei) sind kleiner als
d.h., alle positiven Wurzeln der Gleichung (eine oder drei) sind kleiner als 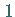 . .
| ![]() ist nicht größer als die
Anzahl der Vorzeichenwechsel in der Koeffizientenfolge des Polynoms
ist nicht größer als die
Anzahl der Vorzeichenwechsel in der Koeffizientenfolge des Polynoms ![]() und kann sich
von dieser nur um eine gerade Zahl unterscheiden.
und kann sich
von dieser nur um eine gerade Zahl unterscheiden.