Komplexe Wurzeln
Komplexe Wurzeln können auch als Lösungen von Polynomgleichungen mit reellen
Koeffizienten auftreten, aber nur paarweise konjugiert komplex, d.h., wenn
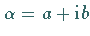 eine Wurzel ist, dann ist auch
eine Wurzel ist, dann ist auch 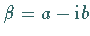 eine, und zwar mit der gleichen Vielfachheit.
Mit
eine, und zwar mit der gleichen Vielfachheit.
Mit 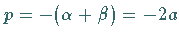 und
und 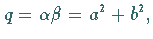 woraus
woraus
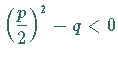 folgt, gilt
folgt, gilt
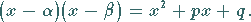 |
(1.168) |
Wird in (1.166a) das Produkt eines jeden Paares derartiger
Faktoren gemäß (1.168) ersetzt, dann ergibt sich eine
Zerlegung des Polynoms mit reellen Koeffizienten in reelle Faktoren
gemäß
Dabei sind 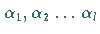 die
die 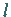 reellen Wurzeln des Polynoms
reellen Wurzeln des Polynoms
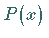 .
Es hat außerdem
.
Es hat außerdem 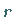 Paare von konjugiert komplexen Wurzeln, die man als Nullstellen
der quadratischen Faktoren
Paare von konjugiert komplexen Wurzeln, die man als Nullstellen
der quadratischen Faktoren 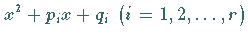 erhält.
Die Zahlen
erhält.
Die Zahlen 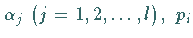 und
und
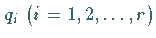 sind reell, und es gilt
sind reell, und es gilt
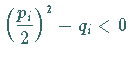 .
.
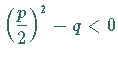 folgt, gilt
folgt, gilt
![]() die
die ![]() reellen Wurzeln des Polynoms
reellen Wurzeln des Polynoms
![]() .
Es hat außerdem
.
Es hat außerdem ![]() Paare von konjugiert komplexen Wurzeln, die man als Nullstellen
der quadratischen Faktoren
Paare von konjugiert komplexen Wurzeln, die man als Nullstellen
der quadratischen Faktoren ![]() erhält.
Die Zahlen
erhält.
Die Zahlen ![]() und
und
![]() sind reell, und es gilt
sind reell, und es gilt
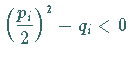 .
.