Fundamentalsatz der Algebra
Jede Gleichung 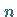 -ten Grades, deren Koeffizienten reelle oder komplexe
Zahlen sind, besitzt
-ten Grades, deren Koeffizienten reelle oder komplexe
Zahlen sind, besitzt 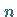 reelle oder komplexe Wurzeln, wobei die
reelle oder komplexe Wurzeln, wobei die 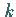 -fachen Wurzeln
-fachen Wurzeln
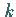 -mal gezählt werden.
Wenn die Wurzeln von
-mal gezählt werden.
Wenn die Wurzeln von 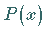 mit
mit 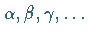 bezeichnet werden und
diese jeweils die Vielfachheiten
bezeichnet werden und
diese jeweils die Vielfachheiten 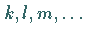 besitzen, dann gilt
die Produktdarstellung
besitzen, dann gilt
die Produktdarstellung
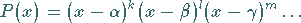 |
(1.166a) |
Die Lösung einer Gleichung 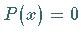 kann stets durch Zurückführen auf eine
Gleichung vereinfacht werden, die die gleichen Wurzeln wie die Ausgangsgleichung hat,
aber jeweils nur noch mit der Vielfachheit 1.
Dazu wird das Polynom in zwei Faktoren derart zerlegt, daß
kann stets durch Zurückführen auf eine
Gleichung vereinfacht werden, die die gleichen Wurzeln wie die Ausgangsgleichung hat,
aber jeweils nur noch mit der Vielfachheit 1.
Dazu wird das Polynom in zwei Faktoren derart zerlegt, daß
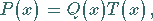 |
(1.166b) |
 |
(1.166c) |
gilt.
Man kann 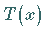 als größten gemeinsamen Teiler der
Polynome
als größten gemeinsamen Teiler der
Polynome 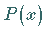 und dessen Ableitung
und dessen Ableitung 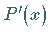 bestimmen, da die mehrfachen Wurzeln
von
bestimmen, da die mehrfachen Wurzeln
von 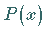 auch Wurzeln von
auch Wurzeln von 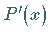 sind.
Das Polynom
sind.
Das Polynom 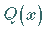 erhält man dann durch Division von
erhält man dann durch Division von 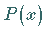 durch
durch 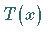 ,
und
,
und
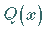 hat dieselben Nullstellen wie
hat dieselben Nullstellen wie 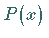 ,
aber mit der Vielfachheit
,
aber mit der Vielfachheit 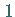 .
.
![]() als größten gemeinsamen Teiler der
Polynome
als größten gemeinsamen Teiler der
Polynome ![]() und dessen Ableitung
und dessen Ableitung ![]() bestimmen, da die mehrfachen Wurzeln
von
bestimmen, da die mehrfachen Wurzeln
von ![]() auch Wurzeln von
auch Wurzeln von ![]() sind.
Das Polynom
sind.
Das Polynom ![]() erhält man dann durch Division von
erhält man dann durch Division von ![]() durch
durch ![]() ,
und
,
und
![]() hat dieselben Nullstellen wie
hat dieselben Nullstellen wie ![]() ,
aber mit der Vielfachheit
,
aber mit der Vielfachheit ![]() .
.