Geometrische Darstellung und Charakteristiken des Systems
Im Falle zweier unabhängiger Veränderlicher 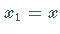 und
und 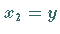 mit
mit
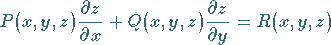 |
(9.71a) |
ist die Lösung 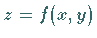 eine Fläche im
eine Fläche im 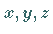 -Raum, die
Integralfläche der Differentialgleichung genannt wird.
Die Gleichung (9.71a) bedeutet, daß in jedem Punkt der
Integralfläche
-Raum, die
Integralfläche der Differentialgleichung genannt wird.
Die Gleichung (9.71a) bedeutet, daß in jedem Punkt der
Integralfläche 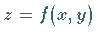 der Normalenvektor
der Normalenvektor
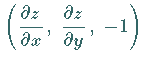 orthogonal zu
dem in diesem Punkt gegebenen Vektor
orthogonal zu
dem in diesem Punkt gegebenen Vektor 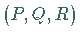 ist.
Dabei nimmt das System (9.70b) die Form
ist.
Dabei nimmt das System (9.70b) die Form
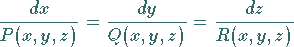 |
(9.71b) |
an.
Daraus folgt (s. Feldlinien eines Vektorfeldes), daß die
Integralkurven des Systems , die auch die
Charakteristiken des Systems genannt werden, die Vektoren 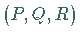 berühren.
Daher liegt eine Charakteristik, die mit der Integralfläche
berühren.
Daher liegt eine Charakteristik, die mit der Integralfläche 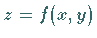 einen Punkt
gemeinsam hat, ganz in dieser Fläche.
Unter der Bedingung, daß der Existenzsatz gilt, verläuft durch
jeden Punkt des Raumes eine Integralkurve des charakteristischen Systems, so daß
die Integralflächen aus Charakteristiken bestehen.
einen Punkt
gemeinsam hat, ganz in dieser Fläche.
Unter der Bedingung, daß der Existenzsatz gilt, verläuft durch
jeden Punkt des Raumes eine Integralkurve des charakteristischen Systems, so daß
die Integralflächen aus Charakteristiken bestehen.
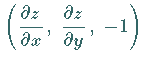 orthogonal zu
dem in diesem Punkt gegebenen Vektor
orthogonal zu
dem in diesem Punkt gegebenen Vektor