Haupteigenschaften der Eigenfunktionen und Eigenwerte
1. Die Eigenwerte eines Randwertproblems bilden eine monoton wachsende Folge
reeller Zahlen
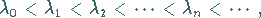 |
(9.65a) |
die gegen unendlich strebt.
2. Die Eigenfunktion, die zum Eigenwert 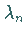 gehört, besitzt im Intervall
gehört, besitzt im Intervall
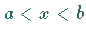 genau
genau  Nullstellen.
Nullstellen.
3. Sind 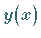 und
und 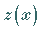 zwei Eigenfunktionen, die zu demselben Eigenwert
zwei Eigenfunktionen, die zu demselben Eigenwert
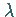 gehören, dann unterscheiden sie sich nur durch einen konstanten Faktor
gehören, dann unterscheiden sie sich nur durch einen konstanten Faktor 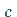 ,
d.h., es gilt
,
d.h., es gilt
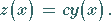 |
(9.65b) |
4. Für zwei Eigenfunktionen 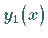 und
und 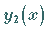 ,
die den verschiedenen
Eigenwerten
,
die den verschiedenen
Eigenwerten 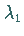 und
und 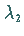 entsprechen, gilt die
Orthogonalitätsrelation
entsprechen, gilt die
Orthogonalitätsrelation
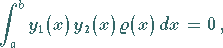 |
(9.65c) |
wobei 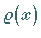 das Gewicht der Orthogonalität genannt wird.
das Gewicht der Orthogonalität genannt wird.
5. Wenn in (9.64a) die Koeffizienten 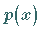 und
und 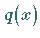 durch
durch
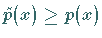 und
und 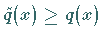 ersetzt werden, dann werden die
Eigenwerte nicht kleiner, sondern es gilt
ersetzt werden, dann werden die
Eigenwerte nicht kleiner, sondern es gilt 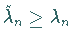 ,
wobei
,
wobei
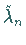 und
und 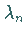 die
die  -ten Eigenwerte der geänderten bzw.
ungeänderten Gleichung sind.
Wenn jedoch der Koeffizient
-ten Eigenwerte der geänderten bzw.
ungeänderten Gleichung sind.
Wenn jedoch der Koeffizient 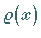 durch
durch 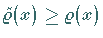 ersetzt wird, dann werden die Eigenwerte nicht größer, sondern es gilt
ersetzt wird, dann werden die Eigenwerte nicht größer, sondern es gilt
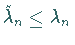 .
Der
.
Der  -te Eigenwert hängt hierbei stetig von den Koeffizienten der Gleichung ab,
d.h., hinreichend kleinen Änderungen der Koeffizienten entsprechen beliebig kleine
Änderungen des
-te Eigenwert hängt hierbei stetig von den Koeffizienten der Gleichung ab,
d.h., hinreichend kleinen Änderungen der Koeffizienten entsprechen beliebig kleine
Änderungen des  -ten Eigenwertes.
-ten Eigenwertes.
6. Verkleinerungen des Intervalls 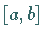 ziehen keine Verkleinerung der Eigenwerte
nach sich.
ziehen keine Verkleinerung der Eigenwerte
nach sich.