Selbstadjungierte Differentialgleichung
Selbstadjungierte Differentialgleichung wird die folgende wichtige Form der
Differentialgleichungen 2. Ordnung genannt:
 |
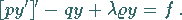(9.64a) |
Als lineare Randbedingungen werden die homogenen Bedingungen
 |
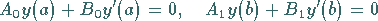(9.64b) |
vorgegeben.
Die Funktionen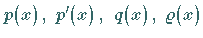 
und 
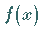sollen in dem
endlichen Intervall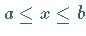 
stetig sein.
Im Falle eines unendlichen Intervalls ändern sich die Ergebnisse ganz wesentlich
(s. Lit. 9.6).
Außerdem wird verlangt, daß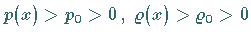 
gilt.
Die Größe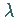 
,
ein Parameter der Differentialgleichung, ist konstant.
Für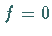 
ergibt sich zum inhomogenen Randwertproblem das zugehörige
homogene Randwertproblem .
Jede Differentialgleichung 2. Ordnung
 |
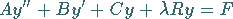(9.64c) |
kann, falls in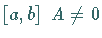 
ist, durch Multiplikation mit 
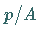auf die
selbstadjungierte Form (9.64a) gebracht werden.
Dazu sind die Substitutionen
 |
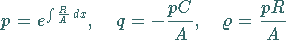(9.64d) |
erforderlich.
Um eine Lösung zu finden, die den inhomogenen Bedingungen
 |
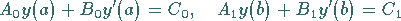(9.64e) |
genügt, geht man auf eine Aufgabe mit homogenen Bedingungen, aber geänderter
rechter Seite der Differentialgleichung, zurück, indem man die unbekannte Funktion
mit Hilfe der Substitution
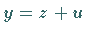ersetzt.
Dabei ist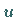 
eine beliebige, zweimal differenzierbare Funktion, die die inhomogenen
Randbedingungen erfüllt, während 
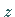eine neue unbekannte Funktion ist, die die
zugehörigen homogenen Randbedingungen erfüllt.
