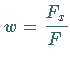Gleichung und Lösungen
Die KdV-Gleichung für die Evolutionsfunktion 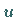 lautet
lautet
 |
(9.134) |
Sie hat die Soliton-Lösung
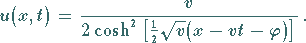 |
(9.135) |
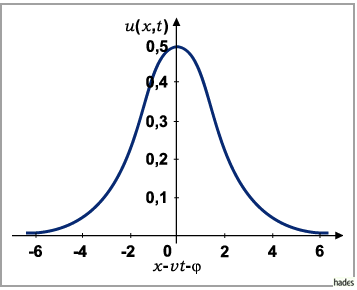
Dieses KdV-Soliton ist durch die zwei dimensionslosen Parameter 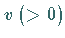 und
und 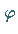 eindeutig bestimmt, und ist in der Abbildung ist
eindeutig bestimmt, und ist in der Abbildung ist  dargestellt.
Ein typisch nichtlinearer Effekt besteht darin, daß die Solitongeschwindigkeit
dargestellt.
Ein typisch nichtlinearer Effekt besteht darin, daß die Solitongeschwindigkeit 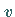 die Amplitude und die Breite des Solitons bestimmt: KdV-Solitonen mit größerer
Amplitude und geringerer Breite bewegen sich schneller als solche mit kleinerer Amplitude
und größerer Breite.
Die Solitonphase
die Amplitude und die Breite des Solitons bestimmt: KdV-Solitonen mit größerer
Amplitude und geringerer Breite bewegen sich schneller als solche mit kleinerer Amplitude
und größerer Breite.
Die Solitonphase 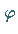 beschreibt die Lage des Maximums des Solitons zur Zeit
beschreibt die Lage des Maximums des Solitons zur Zeit
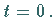
Die Gleichung (9.134) besitzt auch 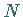 -Solitonenlösungen.
Eine solche
-Solitonenlösungen.
Eine solche 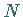 -Solitonenlösung läßt sich für
-Solitonenlösung läßt sich für 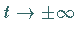 asymptotisch durch lineare Überlagerung von Ein-Solitonlösungen darstellen:
asymptotisch durch lineare Überlagerung von Ein-Solitonlösungen darstellen:
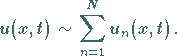 |
(9.136) |
Dabei ist jede Evolutionsfunktion 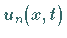 durch eine Geschwindigkeit
durch eine Geschwindigkeit 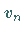 und eine
Phase
und eine
Phase 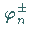 gekennzeichnet.
Die Anfangsphasen
gekennzeichnet.
Die Anfangsphasen 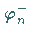 vor der Wechselwirkung oder dem Stoßprozeß
unterscheiden sich von den Endphasen nach dem Stoß
vor der Wechselwirkung oder dem Stoßprozeß
unterscheiden sich von den Endphasen nach dem Stoß 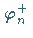 ,
während die
Geschwindigkeiten
,
während die
Geschwindigkeiten 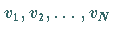 keine Änderung erfahren, d.h., es handelt
sich um eine elastische Wechselwirkung.
keine Änderung erfahren, d.h., es handelt
sich um eine elastische Wechselwirkung.
Für 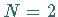 besitzt (9.134) eine 2-Solitonenlösung.
Sie läßt sich für endliche Zeiten nicht durch lineare Überlagerung darstellen
und lautet mit
besitzt (9.134) eine 2-Solitonenlösung.
Sie läßt sich für endliche Zeiten nicht durch lineare Überlagerung darstellen
und lautet mit 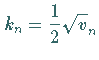 und
und
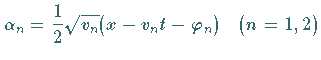 :
:
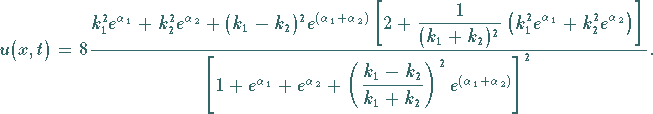 |
(9.137) |
Diese Gleichung (9.137) beschreibt asymptotisch zwei für
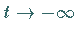 nicht wechselwirkende Solitonen mit den Geschwindigkeiten
nicht wechselwirkende Solitonen mit den Geschwindigkeiten
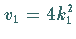 und
und 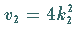 ,
die nach einem Wechselwirkungsprozeß für
,
die nach einem Wechselwirkungsprozeß für
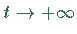 wieder asymptotisch in zwei nichtwechselwirkende Solitonen mit
denselben Geschwindigkeiten übergehen.
wieder asymptotisch in zwei nichtwechselwirkende Solitonen mit
denselben Geschwindigkeiten übergehen.
Die nichtlineare Evolutionsgleichung
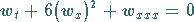 |
(9.138a) |
hat mit 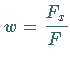
a) für
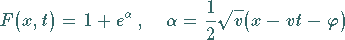 |
(9.138b) |
eine Solitonlösung und
b) für
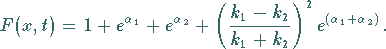 |
(9.138c) |
eine 2-Solitonenlösung.
Mit 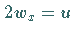 ergibt sich aus (9.138a) die KdV-Gleichung
(9.134).
Die Gleichung (9.137) und der sich mit (9.138c)
ergebende Ausdruck für
ergibt sich aus (9.138a) die KdV-Gleichung
(9.134).
Die Gleichung (9.137) und der sich mit (9.138c)
ergebende Ausdruck für 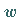 sind Beispiele für eine nichtlineare Superposition.
sind Beispiele für eine nichtlineare Superposition.
Ersetzt man in (9.134) den Term 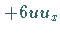 durch
durch 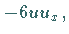 so muß
die rechte Seite von (9.135) mit
so muß
die rechte Seite von (9.135) mit 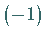 multiplizieren werden.
Man spricht dann auch von einem Antisoliton .
multiplizieren werden.
Man spricht dann auch von einem Antisoliton .
![]() -Solitonenlösungen.
Eine solche
-Solitonenlösungen.
Eine solche ![]() -Solitonenlösung läßt sich für
-Solitonenlösung läßt sich für ![]() asymptotisch durch lineare Überlagerung von Ein-Solitonlösungen darstellen:
asymptotisch durch lineare Überlagerung von Ein-Solitonlösungen darstellen:
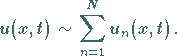
![]() durch eine Geschwindigkeit
durch eine Geschwindigkeit ![]() und eine
Phase
und eine
Phase ![]() gekennzeichnet.
Die Anfangsphasen
gekennzeichnet.
Die Anfangsphasen ![]() vor der Wechselwirkung oder dem Stoßprozeß
unterscheiden sich von den Endphasen nach dem Stoß
vor der Wechselwirkung oder dem Stoßprozeß
unterscheiden sich von den Endphasen nach dem Stoß ![]() ,
während die
Geschwindigkeiten
,
während die
Geschwindigkeiten ![]() keine Änderung erfahren, d.h., es handelt
sich um eine elastische Wechselwirkung.
keine Änderung erfahren, d.h., es handelt
sich um eine elastische Wechselwirkung.
![]() besitzt (9.134) eine 2-Solitonenlösung.
Sie läßt sich für endliche Zeiten nicht durch lineare Überlagerung darstellen
und lautet mit
besitzt (9.134) eine 2-Solitonenlösung.
Sie läßt sich für endliche Zeiten nicht durch lineare Überlagerung darstellen
und lautet mit 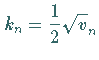 und
und
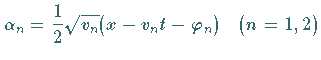 :
: