Inhomogene Bedingungen und inhomogene Differentialgleichungen
Die Lösung homogener oder inhomogener linearer partieller Differentialgleichungen bei
inhomogenen Anfangs- oder Randbedingungen kann auf die Lösung einer Gleichung
zurückgeführt werden, die sich von der gegebenen lediglich durch das die unbekannte
Funktion nicht mehr enthaltende freie Glied unterscheidet, jetzt aber bei homogenen
Bedingungen.
Dazu reicht es aus, die zu bestimmende Funktion durch eine Differenz zwischen ihr und
einer beliebigen, zweimal differenzierbaren Funktion zu ersetzen, die die gegebenen
inhomogenen Bedingungen erfüllt.
Generell wird von der Erkenntnis Gebrauch gemacht, daß sich die Lösung einer
linearen inhomogenen partiellen Differentialgleichung bei gegebenen inhomogenen Anfangs-
oder Randbedingungen als Summe der Lösung der gleichen Differentialgleichung bei
Nullbedingungen und der Lösung der entsprechenden homogenen Differentialgleichung bei
den gegebenen Bedingungen darstellen läßt.
Zur Zurückführung der Lösung der linearen inhomogenen partiellen
Differentialgleichung
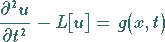 |
(9.101a) |
bei den homogenen Anfangsbedingungen
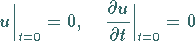 |
(9.101b) |
auf die Lösung des CAUCHYschen Problems für die zugehörige homogene
Differentialgleichung wird
 |
(9.101c) |
gesetzt.
Dabei ist 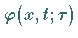 die Lösung der Differentialgleichung
die Lösung der Differentialgleichung
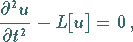 |
(9.101d) |
die den Randbedingungen
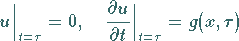 |
(9.101e) |
genügt.
In diesen Gleichungen steht 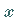 symbolisch für die Gesamtheit der
symbolisch für die Gesamtheit der  Variablen
Variablen
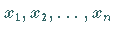 des
des  -dimensionalen Problems.
Mit
-dimensionalen Problems.
Mit 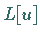 wird dabei ein linearer Differentialausdruck bezeichnet, der die Ableitung
wird dabei ein linearer Differentialausdruck bezeichnet, der die Ableitung
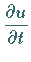 enthalten darf, nicht aber höhere Ableitungen nach
enthalten darf, nicht aber höhere Ableitungen nach 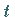 .
.
