Hinreichende Bedingung für die Konvergenz eines uneigentlichen Integrals mit unbeschränktem Integranden
1. Wenn das Integral 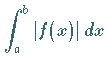 existiert, dann
existiert auch das Integral
existiert, dann
existiert auch das Integral 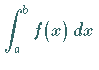 .
Man spricht in diesem Falle vom absolut konvergenten Integral und von der
absolut integrierbaren Funktion
.
Man spricht in diesem Falle vom absolut konvergenten Integral und von der
absolut integrierbaren Funktion 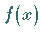 in dem betreffenden Intervall.
in dem betreffenden Intervall.
2. Wenn die Funktion 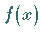 in dem Intervall
in dem Intervall 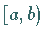 positiv ist, und wenn es
eine Zahl
positiv ist, und wenn es
eine Zahl 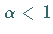 derart gibt, daß für hinreichend nahe bei
derart gibt, daß für hinreichend nahe bei 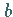 gelegene
gelegene
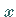 -Werte gilt
-Werte gilt
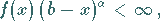 |
(8.89a) |
dann konvergiert das Integral (8.87a).
Wenn jedoch 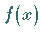 im Intervall
im Intervall 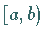 positiv ist und eine Zahl
positiv ist und eine Zahl 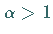 derart
existiert, daß für hinreichend nahe bei
derart
existiert, daß für hinreichend nahe bei 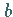 gelegene
gelegene 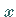 -Werte gilt
-Werte gilt
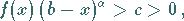 |
(8.89b) |
dann divergiert das Integral (8.87a).
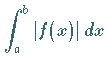 existiert, dann
existiert auch das Integral
existiert, dann
existiert auch das Integral 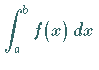 .
Man spricht in diesem Falle vom absolut konvergenten Integral und von der
absolut integrierbaren Funktion
.
Man spricht in diesem Falle vom absolut konvergenten Integral und von der
absolut integrierbaren Funktion