Oberflächenintegral allgemeiner Art
Wenn in einem zusammenhängenden Gebiet drei Funktionen mit den drei Veränderlichen
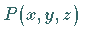 ,
,
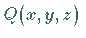 ,
,
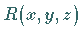 und ein orientiertes Flächenstück
und ein orientiertes Flächenstück  gegeben
sind, dann wird als Oberflächenintegral allgemeiner Art die Summe der Integrale zweiter
Art über alle Projektionen bezeichnet:
gegeben
sind, dann wird als Oberflächenintegral allgemeiner Art die Summe der Integrale zweiter
Art über alle Projektionen bezeichnet:
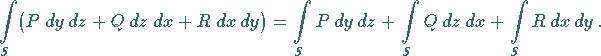 |
(8.162) |
Die allgemeine Formel, mit deren Hilfe man das Oberflächenintegral allgemeiner Art auf
das gewöhnliche Doppelintegral zurückführt, lautet:
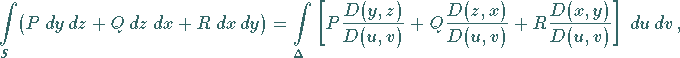 |
(8.163) |
wobei die Größen
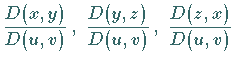 und
und 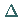 die oben angegebene Bedeutung besitzen.
die oben angegebene Bedeutung besitzen.
Die vektorielle Darlegung der Theorie des Oberflächenintegrals allgemeiner Art ist
im Kapitel Feldtheorie enthalten.
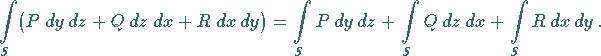
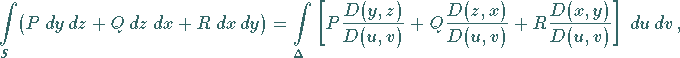
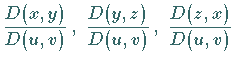 und
und