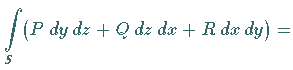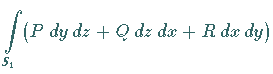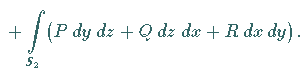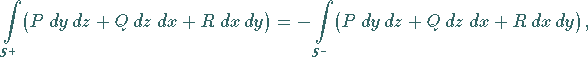Eigenschaften des Oberflächenintegrals
1. Wenn das Integrationsgebiet, d.h. das Flächenstück 
,
auf irgendeine
Art in Teilflächenstücke 
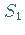und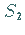 
eingeteilt ist, dann gilt:
2. Bei Vertauschung von Außen- und Innenseite der Fläche, d.h. bei
Änderung der Orientierung der Fläche, ändert das Integral sein Vorzeichen:
 |
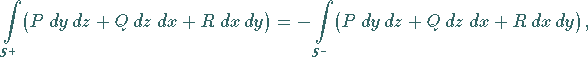(8.165) |
wobei mit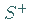 
und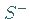 
ein und dieselbe Fläche bezeichnet ist, jedoch für
entgegengesetzte Orientierung.
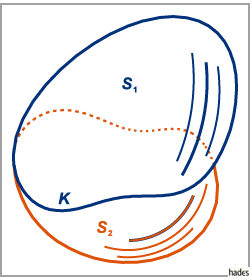
3. Im allgemeinen hängt das Oberflächenintegral sowohl von der das
Flächenstück
begrenzenden Kurve als auch von der Fläche selbst ab.
Daher sind die Integrale über verschiedene nichtgeschlossene Flächen
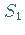und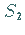
mit der gleichen Randkurve 
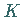im allgemeinen verschieden (s. Abbildung):
 |
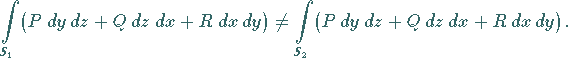(8.166) |
