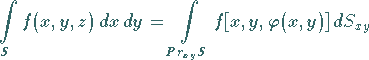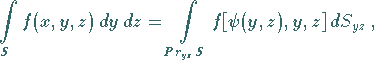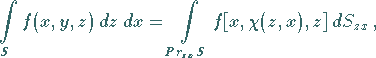Ist die Fläche 
durch die Gleichung
 |
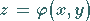(8.158) |
explizit vorgegeben, dann wird das Integral (8.157a) nach der
Formel
 |
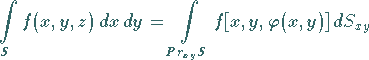(8.159a) |
berechnet, wobei gilt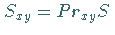 
.
Die Oberflächenintegrale der Funktion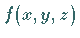 
über die Projektionen des
Flächenstückes
auf die anderen Koordinatenebenen werden analog berechnet:
 |
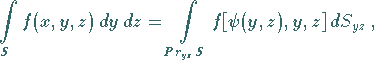(8.159b) |
wobei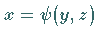 
die Gleichung der Fläche
nach 
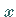aufgelöst ist und
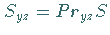zu setzen ist.
 |
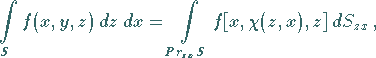(8.159c) |
wobei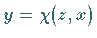 
die nach 
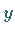aufgelöste Gleichung der Fläche
ist und
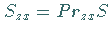zu setzen ist.
Wenn die Orientierung der Fläche geändert wird, d.h., wenn die Außen- mit der
Innenseite vertauscht wird, dann ändert das Integral über die Projektion sein
Vorzeichen.
