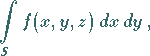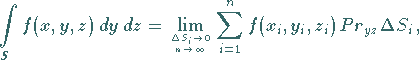Definition des Oberflächenintegrals 2. Art über eine Projektion auf eine Koordinatenebene
Oberflächenintegral 2. Art einer Funktion von drei Veränderlichen
,
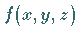die in einem zusammenhängenden Gebiet definiert ist, nennt man das
Integral
 |
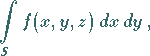(8.156) |
das über die Projektion auf die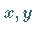 
-Ebene eines orientierten, in dem gleichen Gebiet
liegenden Flächenstückes 
genomen wird.
Der Zahlenwert des Integrals wird ebenso gewonnen, wie der des Oberflächenintegrals
1. Art, ausgenommen den dritten Schritt, bei dem der Funktionswert
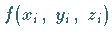nicht mit dem Flächenelement 
,
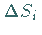sondern mit
dessen Projektion 
,
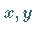orientiert auf die -Ebene, zu
multiplizieren ist.
Damit ergibt sich:
 |
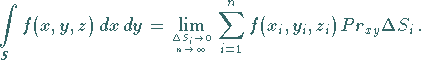(8.157a) |
In Analogie dazu werden die Oberflächenintegrale 2. Art über die Projektionen
des orientierten Flächenstückes
auf die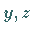 
- und die 
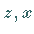-Ebene wie folgt
berechnet:
 |
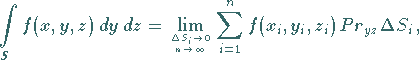(8.157b) |
 |
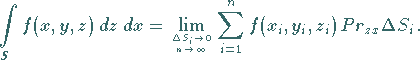(8.157c) |
