Explizite Darstellung der Fläche
Ist die Fläche  durch die Gleichung
durch die Gleichung
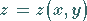 |
(8.150) |
explizit vorgegeben, dann gilt
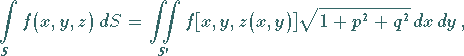 |
(8.151a) |
wobei 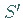 die Projektion von
die Projektion von  auf die
auf die 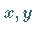 -Ebene ist und
-Ebene ist und 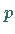 und
und 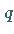 die partiellen
Ableitungen
die partiellen
Ableitungen 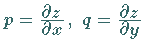 sind.
Dabei wird vorausgesetzt, daß jedem Punkt der Fläche
sind.
Dabei wird vorausgesetzt, daß jedem Punkt der Fläche  in der
in der 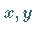 -Ebene
eindeutig ein Punkt ihrer Projektion
-Ebene
eindeutig ein Punkt ihrer Projektion 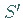 entspricht, d.h., der Flächenpunkt muß
eindeutig durch seine Koordinaten definiert sein.
Sollte das nicht der Fall sein, dann wird das Flächenstück
entspricht, d.h., der Flächenpunkt muß
eindeutig durch seine Koordinaten definiert sein.
Sollte das nicht der Fall sein, dann wird das Flächenstück  in einige
Teilflächenstücke eingeteilt, so daß das Integral über die gesamte Fläche als
algebraische Summe der Integrale über die Teilflächenstücke von
in einige
Teilflächenstücke eingeteilt, so daß das Integral über die gesamte Fläche als
algebraische Summe der Integrale über die Teilflächenstücke von  dargestellt
werden kann.
Ist die Fläche in Parameterform gegeben, dann entfällt diese Einschränkung.
dargestellt
werden kann.
Ist die Fläche in Parameterform gegeben, dann entfällt diese Einschränkung.
Die Gleichung (8.151a) kann auch in der anderen Form
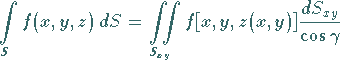 |
(8.151b) |
dargestellt werden.
Das hängt damit zusammen, daß die Gleichung der Flächennormalen von
(8.150) die Form
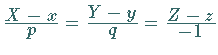 hat, so daß
für den Winkel zwischen der Normalenrichtung und der
hat, so daß
für den Winkel zwischen der Normalenrichtung und der 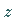 -Achse die Beziehung
-Achse die Beziehung
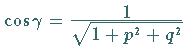 besteht.
Bei der Berechnung eines Oberflächenintegrals 1. Art faßt man diesen Winkel
besteht.
Bei der Berechnung eines Oberflächenintegrals 1. Art faßt man diesen Winkel
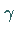 als spitzen Winkel auf, so daß immer
als spitzen Winkel auf, so daß immer 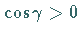 ist.
ist.
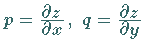 sind.
Dabei wird vorausgesetzt, daß jedem Punkt der Fläche
sind.
Dabei wird vorausgesetzt, daß jedem Punkt der Fläche 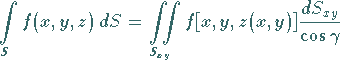
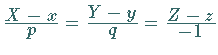 hat, so daß
für den Winkel zwischen der Normalenrichtung und der
hat, so daß
für den Winkel zwischen der Normalenrichtung und der 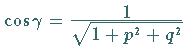 besteht.
Bei der Berechnung eines Oberflächenintegrals 1. Art faßt man diesen Winkel
besteht.
Bei der Berechnung eines Oberflächenintegrals 1. Art faßt man diesen Winkel