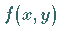|
|
|
|
bzw.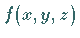 
sowie die Kurve längs des Bogenstückes 
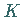stetig
sind und die Kurve dort eine stetige Tangente besitzt.
Anders formuliert: Es existieren in diesem Falle die genannten Grenzwerte, und sie sind
unabhängig von der Wahl der Punkte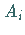 
und 
.
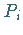Die Funktion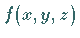
heißt in diesem Falle längs der Kurve
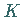integrierbar.
|
|