Definition des Kurvenintegrals 1. Art
Kurvenintegral 1. Art oder Integral über eine Bogenlänge
wird das bestimmte Integral
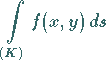 |
(8.106) |
genannt, wobei 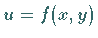 eine in einem zusammenhängenden Gebiet definierte
Funktion von zwei Veränderlichen ist und die Integration über den Kurvenbogen
eine in einem zusammenhängenden Gebiet definierte
Funktion von zwei Veränderlichen ist und die Integration über den Kurvenbogen
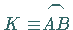 einer ebenen, durch ihre Gleichung vorgegebenen Kurve durchgeführt
wird.
Das betreffende Bogenstück liegt in dem gleichen Gebiet und wird Integrationsweg genannt.
Der Zahlenwert des Kurvenintegrals 1. Art wird auf die folgende Weise ermittelt
(s. Abbildung).
einer ebenen, durch ihre Gleichung vorgegebenen Kurve durchgeführt
wird.
Das betreffende Bogenstück liegt in dem gleichen Gebiet und wird Integrationsweg genannt.
Der Zahlenwert des Kurvenintegrals 1. Art wird auf die folgende Weise ermittelt
(s. Abbildung).
1. Zerlegung des Bogenstückes 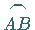 in
in 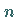 Elemementarbogenstücke
durch beliebig gewählte Punkte
Elemementarbogenstücke
durch beliebig gewählte Punkte  ,
beginnend beim
Anfangspunkt
,
beginnend beim
Anfangspunkt 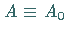 bis zum Endpunkt
bis zum Endpunkt  .
.
2. Auswahl beliebiger Punkte 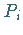 im Innern oder auf dem Rande eines jeden
Elementarbogenstückes
im Innern oder auf dem Rande eines jeden
Elementarbogenstückes 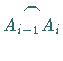 mit den Koordinaten
mit den Koordinaten 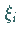 und
und
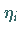 .
.
3. Multiplikation der Funktionswerte 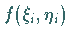 in den gewählten
Punkten mit den positiv zu nehmenden Bogenlängen
in den gewählten
Punkten mit den positiv zu nehmenden Bogenlängen
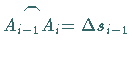 .
.
4. Addition aller so gewonnenen 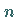 Produkte
Produkte
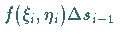 .
.
5. Berechnung des Grenzwertes der Summe
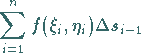 |
(8.107a) |
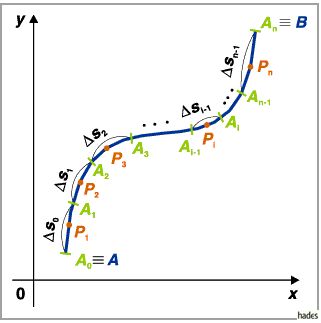
für den Fall, daß die Länge jedes Elementarbogenstückes 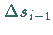 gegen Null geht, also
gegen Null geht, also 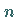 gegen
gegen  .
.
Wenn der Grenzwert von (8.107a) existiert und unabhängig ist
von der Wahl der Punkte 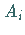 und
und 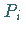 ,
so wird er
Kurvenintegral 1. Art genannt, und man schreibt
,
so wird er
Kurvenintegral 1. Art genannt, und man schreibt
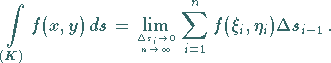 |
(8.107b) |
In Analogie dazu wird das Kurvenintegral 1. Art für eine Funktion 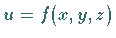 von drei Veränderlichen definiert, dessen Integrationsweg das Bogenstück einer
Raumkurve ist:
von drei Veränderlichen definiert, dessen Integrationsweg das Bogenstück einer
Raumkurve ist:
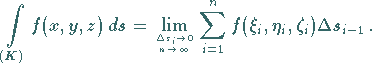 |
(8.107c) |
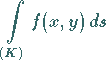
![]() eine in einem zusammenhängenden Gebiet definierte
Funktion von zwei Veränderlichen ist und die Integration über den Kurvenbogen
eine in einem zusammenhängenden Gebiet definierte
Funktion von zwei Veränderlichen ist und die Integration über den Kurvenbogen
![]() einer ebenen, durch ihre Gleichung vorgegebenen Kurve durchgeführt
wird.
Das betreffende Bogenstück liegt in dem gleichen Gebiet und wird Integrationsweg genannt.
Der Zahlenwert des Kurvenintegrals 1. Art wird auf die folgende Weise ermittelt
(s. Abbildung).
einer ebenen, durch ihre Gleichung vorgegebenen Kurve durchgeführt
wird.
Das betreffende Bogenstück liegt in dem gleichen Gebiet und wird Integrationsweg genannt.
Der Zahlenwert des Kurvenintegrals 1. Art wird auf die folgende Weise ermittelt
(s. Abbildung).
![]() in
in ![]() Elemementarbogenstücke
durch beliebig gewählte Punkte
Elemementarbogenstücke
durch beliebig gewählte Punkte ![]() ,
beginnend beim
Anfangspunkt
,
beginnend beim
Anfangspunkt ![]() bis zum Endpunkt
bis zum Endpunkt ![]() .
.
![]() im Innern oder auf dem Rande eines jeden
Elementarbogenstückes
im Innern oder auf dem Rande eines jeden
Elementarbogenstückes 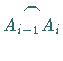 mit den Koordinaten
mit den Koordinaten ![]() und
und
![]() .
.
![]() in den gewählten
Punkten mit den positiv zu nehmenden Bogenlängen
in den gewählten
Punkten mit den positiv zu nehmenden Bogenlängen
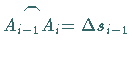 .
.
![]() Produkte
Produkte
![]() .
.