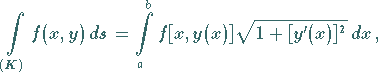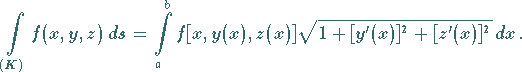Berechnung des Kurvenintegrals 1. Art
Die Berechnung des Kurvenintegrals 1. Art erfolgt durch Zurückführung auf die
Berechnung des bestimmten Integrals.
1. Vorgabe der Gleichung des Integrationsweges in Parameterform:
Lauten die Gleichungen eines ebenen Integrationsweges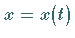 
und 
,
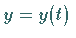dann
gilt
 |
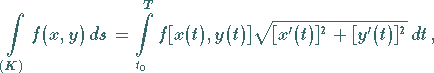(8.108a) |
und im Falle eines räumlichen Integrationsweges mit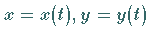 
und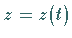 
 |
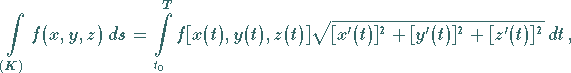(8.108b) |
wobei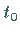 
der Wert des Parameters 
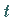im Punkt 
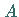und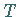 
sein Wert für den Punkt
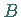ist.
Die Punkte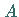
und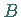
werden so gewählt, daß die Bedingung 
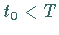erfüllt
ist.
2. Vorgabe der Gleichung des Integrationsweges in expliziter Form:
Man setzt 
und erhält aus (8.108a) im ebenen Falle
 |
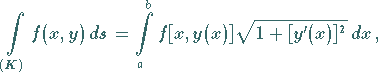(8.109a) |
und aus (8.108b) im räumlichen Falle
 |
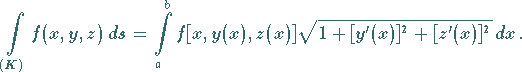(8.109b) |
Dabei si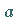nd 
und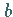 
die Abszissen der Punkte
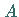und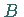 
,
wobei die Bedingung
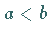erfüllt sein muß.
Außerdem wird angenommen, daß jedem Punkt der Projektion des Kurvenstückes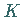 
auf die 
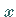-Achse dort eindeutig ein Punkt entspricht, d.h., daß jeder Kurvenpunkt
eindeutig durch einen Abszissenpunkt bestimmt wird.
Wenn das nicht der Fall ist, dann wird das Bogenstück in mehrere Teilintervalle zerlegt,
von denen jedes die genannte Eigenschaft besitzt.
Das Kurvenintegral über das gesamte Kurvenstück ist dann gleich der Summe der
Kurvenintegrale über die Teilintervalle.
