Geometrisch betrachtet gehört zu einem relativen Extremwert einer Funktion zweier
Veränderlicher, die in einem kartesischen Koordinatensystem
als Fläche dargestellt ist, ein Punkt  ,
in dem die
Applikate der Fläche größer bzw. kleiner ist als die
Applikate aller beliebigen anderen Punkte in hinreichend kleiner Entfernung vom Punkt
,
in dem die
Applikate der Fläche größer bzw. kleiner ist als die
Applikate aller beliebigen anderen Punkte in hinreichend kleiner Entfernung vom Punkt
 ,
d.h. in einem Gebiet kleiner Ausdehnung, das den Punkt
,
d.h. in einem Gebiet kleiner Ausdehnung, das den Punkt  enthält.
enthält.
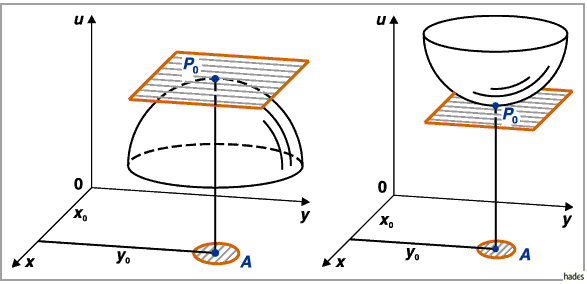
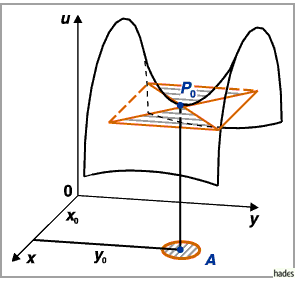
Wenn die Fläche im Punkt 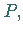 der ein relatives Extremum darstellt, eine Tangentialebene
besitzt, dann verläuft diese parallel zur
der ein relatives Extremum darstellt, eine Tangentialebene
besitzt, dann verläuft diese parallel zur 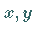 -Ebene (linke und rechte Abbildung).
Diese Bedingung ist notwendig, aber nicht hinreichend dafür, daß im Punkt
-Ebene (linke und rechte Abbildung).
Diese Bedingung ist notwendig, aber nicht hinreichend dafür, daß im Punkt 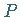 ein
Maximum oder Minimum vorhanden ist.
In der unteren Abbildung zeichnet sich die Fläche im Punkt
ein
Maximum oder Minimum vorhanden ist.
In der unteren Abbildung zeichnet sich die Fläche im Punkt 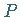 durch eine horizontale
Tangentialebene aus, doch besitzt die Funktion dort kein Extremum, sondern einen
Sattelpunkt.
durch eine horizontale
Tangentialebene aus, doch besitzt die Funktion dort kein Extremum, sondern einen
Sattelpunkt.