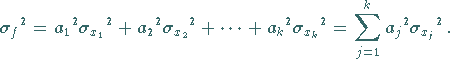Da die Fehler relativ kleine Änderungen der unabhängigen Variablen darstellen, kann
die Funktion 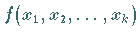 in der Nähe der Mittelwerte
in der Nähe der Mittelwerte 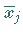 durch den Linearanteil ihrer TAYLOR-Entwicklung mit den Koeffizienten
durch den Linearanteil ihrer TAYLOR-Entwicklung mit den Koeffizienten 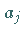 angenähert werden, so daß für ihren Fehler
angenähert werden, so daß für ihren Fehler 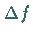 gilt:
gilt:
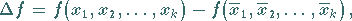 |
(16.223a) |
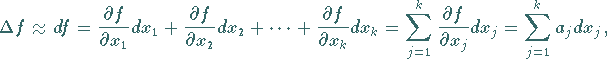 |
(16.223b) |
wobei die partiellen Ableitungen 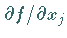 an der Stelle
an der Stelle
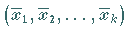 zu nehmen sind.
zu nehmen sind.
Streuung und Standardabweichung der Funktion ergeben sich zu
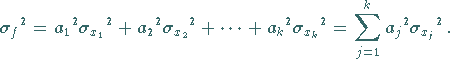 |
(16.224) |