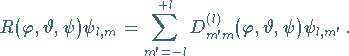Drehgruppe SO(3)
Gemäß (5.145) spannen die Komponenten des Bahndrehimpulsoperators
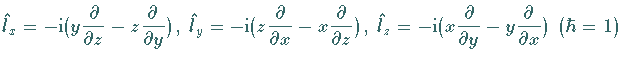 die LIE-Algebra
die LIE-Algebra 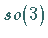 der Drehgruppe
der Drehgruppe 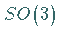 auf, so daß sich eine
Funktion
auf, so daß sich eine
Funktion 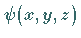 bei infinitesimalen Drehungen mit dem Winkel
bei infinitesimalen Drehungen mit dem Winkel 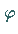 um
die
um
die 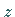 -Achse gemäß
-Achse gemäß
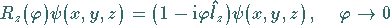 |
(5.162) |
transformiert.
Da alle infinitesimalen Generatoren nicht untereinander kommutieren,
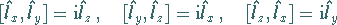 |
(5.163) |
erhält man für den Rang von 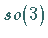 den Wert
den Wert 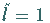 ,
d.h., in
,
d.h., in
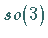 kann eine Basis so gewählt werden, daß höchstens einer der drei
Generatoren durch eine Diagonalmatrix dargestellt wird.
Als Standardbasis wird im allgemeinen
kann eine Basis so gewählt werden, daß höchstens einer der drei
Generatoren durch eine Diagonalmatrix dargestellt wird.
Als Standardbasis wird im allgemeinen
 |
(5.164) |
eingeführt, wobei 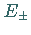 die Leiteroperatoren sind.
die Leiteroperatoren sind.
Nach dieser Basistransformation
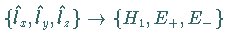 gelten für die
Elemente der neuen Basis
gelten für die
Elemente der neuen Basis
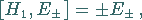 |
(5.165a) |
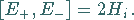 |
(5.165b) |
Der Raum, in dem die Wurzeln und Gewichte der LIE-Algebra 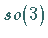 dargestellt
werden können, ist eindimensional
dargestellt
werden können, ist eindimensional 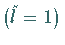 .
Gemäß (5.165a) besteht das System der Wurzelvektoren aus
.
Gemäß (5.165a) besteht das System der Wurzelvektoren aus
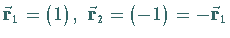 .
.

Die Gewichte 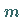 der inäquivalenten irreduziblen Darstellungen von
der inäquivalenten irreduziblen Darstellungen von 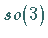 (und damit von
(und damit von 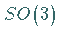 )
sind ganzzahlig und unterscheiden sich um
)
sind ganzzahlig und unterscheiden sich um 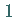 .
Das höchste Gewicht einer irreduziblen Darstellung von
.
Das höchste Gewicht einer irreduziblen Darstellung von 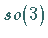 sei
sei
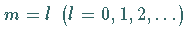 ,
der zugehörige Eigenvektor wird mit
,
der zugehörige Eigenvektor wird mit
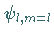 bezeichnet.
Die Eigenvektoren zu möglichen anderen Gewichten erhält man durch sukzessive
Anwendung des Leiteroperators
bezeichnet.
Die Eigenvektoren zu möglichen anderen Gewichten erhält man durch sukzessive
Anwendung des Leiteroperators 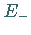 auf
auf 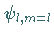 bis der Eigenvektor zu
bis der Eigenvektor zu
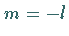 erreicht ist
erreicht ist 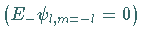 .
In jedem Schritt wird das Gewicht gemäß (5.161) reduziert von
.
In jedem Schritt wird das Gewicht gemäß (5.161) reduziert von 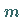 auf
auf 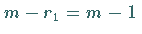 .
Das Gewichtsdiagramm einer irreduziblen Darstellung
.
Das Gewichtsdiagramm einer irreduziblen Darstellung 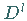 von
von 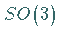 mit dem
höchsten Gewicht
mit dem
höchsten Gewicht 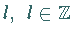 besteht also aus allen Punkten
besteht also aus allen Punkten
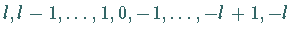 auf der Zahlengeraden (s. obige Abbildung).
auf der Zahlengeraden (s. obige Abbildung).
Die Darstellung ist damit 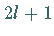 -dimensional.
Die Basisvektoren im Darstellungsraum sind die Eigenfunktionen
-dimensional.
Die Basisvektoren im Darstellungsraum sind die Eigenfunktionen 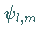 des
Operators
des
Operators 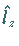 der
der 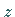 -Komponente des Bahndrehimpulses zum Eigenwert
-Komponente des Bahndrehimpulses zum Eigenwert 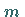 ,
,
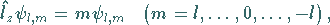 |
(5.166) |
so daß die Gewichte 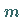 der irreduziblen Darstellung von
der irreduziblen Darstellung von 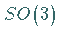 physikalisch die
möglichen Meßwerte für die Projektion des Bahndrehimpulses
physikalisch die
möglichen Meßwerte für die Projektion des Bahndrehimpulses 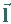 auf
die Quantisierungsachse (
auf
die Quantisierungsachse (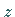 -Achse) bedeuten (Richtungsquantelung).
Da der CASIMIR-Operator
-Achse) bedeuten (Richtungsquantelung).
Da der CASIMIR-Operator 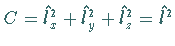 mit allen Generatoren kommutiert,
mit allen Generatoren kommutiert,
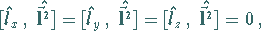 |
(5.167) |
sind die Funktionen 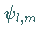 auch Eigenfunktionen zum Quadrat des
Drehimpulsoperators.
Die Eigenwerte sind
auch Eigenfunktionen zum Quadrat des
Drehimpulsoperators.
Die Eigenwerte sind 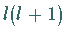 :
:
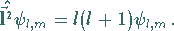 |
(5.168) |
Die Zahl 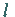 ,
die die irreduzible Darstellung von
,
die die irreduzible Darstellung von 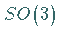 spezifiziert, legt
also noch den Betrag
spezifiziert, legt
also noch den Betrag 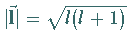 des Drehimpulses
des Drehimpulses 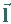 fest.
fest.
Bei endlichen dreidimensionalen Drehungen 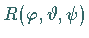 um die
EULERschen Winkel
um die
EULERschen Winkel 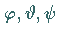 transformieren sich die Funktionen
transformieren sich die Funktionen
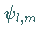 untereinander gemäß
untereinander gemäß
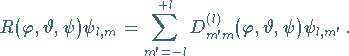 |
(5.169) |
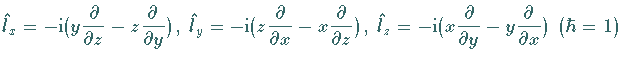 die LIE-Algebra
die LIE-Algebra